Extended Source Analysis with ASCA

T. Takahashi^1,2, M. Markevitch^1,6,
Y. Fukazawa², Y. Ikebe^2,3,
Y. Ishisaki², K. Kikuchi⁴,
K. Makishima², Y. Tawara⁵,
and ASCA Image analysis working group

¹ Institute of Space and Astronautical Science
² Dept. of Physics, Univ. of Tokyo
³ Riken
⁴ Dept. of Physics, Tokyo Metropolitan Univ.
⁵ Dept. of Physics, Nagoya Univ.
⁶ Moscow

takahasi@astro.isas.jaxa.jp

ASCA mirrors have a wide energy- and position-dependent point spread function (PSF), which must be accurately taken into account to fully utilize the spectro-imaging capability of the telescope. Below we discuss effects of the PSF, how it was calibrated, and how it can be included in the analysis of the extended sources.

Figure 1: Cyg X-1 smoothed images from GIS2 at theta=8', at soft and hard energies. A plus marks the optical axis position. Circles contain 90% of all photons within the 16' radius in each image; they are of 6' radius for the soft image and 10' for the hard image. At higher energy, the PSF has wider outskirts.

Figure 2: Smoothed 0.5-10 keV images of Cyg X-1 at different focal plane positions: (1) off-axis distance theta=2', (2) theta=13', and (3) theta=17'. Contours are logarithmically spaced. The PSF position dependence is strong -- the image becomes more distorted at greater off-axis distances.

Naïve methods of extended source analysis (e.g., fitting spectra from the concentric rings around the cluster center, with the XRT ancillary response calculated for each ring individually) do not work with ASCA (Takahashi et al. 1994). For clusters with relatively small angular sizes which are within the GIS field of view, the outer rings, however large, inevitably have a non-negligible energy-dependent contribution of the flux from the inner brighter parts. For example, for a symmetric cluster with ax=1.2' and beta=0.62 divided into concentric rings 0'-4'-8'-12', the flux in the outer ring is in fact dominated by that scattered from the inner cluster part. Fractions of the flux from the inner, middle and outer rings in the sky are (0.94, 0.06, 0.002) in the inner image ring, (0.55, 0.42, 0.04) in the second ring, and (0.33, 0.29, 0.39) in the outer ring for E=2.5 keV, respectively, while for E=10 keV, the respective fractions are (0.93, 0.06, 0.004), (0.57, 0.39, 0.04), and (0.48, 0.25, 0.27). These numbers show that even though the image rings are much larger than the PSF half-power diameter, flux from the inner cluster regions can be extremely important in the outer rings. One also notices that the sign of the energy dependence of these fractions is such that, if these effects are not accounted for, the outer part of an isothermal cluster would look hotter, as is seen in Figure 3 which shows a temperature profile of the simulated isothermal cluster obtained by a naïve method ignoring the PSF effects. To take this scattering into account, an accurate two-dimensional energy-dependent model of the mirror PSF should be included in the analysis. Eventually, such a model will be created using the upgraded raytracing code. In the meantime, we suggest to use a model obtained by interpolation between a set of actual GIS Cyg X-1 images as described below.

Figure 3: A simulated isothermal symmetric cluster with ax=1' and beta=0.55 is divided into concentric rings, whose spectra are fit individually ignoring the PSF scattering. Different symbols correspond to different true temperatures. The cluster is simulated using the PSF model reconstructed from Cyg X-1 images (see text). A spurious temperature increase outward arises because the PSF is wider at higher energies.

Calibration of the PSF

To calibrate the mirror PSF, we have used the observations of Cyg X-1 performed in November 1993, November 1994 and May 1995 at several offset positions. This source is bright and hard and provides sufficient statistics to obtain high quality GIS images in the narrow energy intervals. Utilizing the 5' relative misalignment between the two GIS mirrors, the obtained pointings sample the PSF for a total of 13 focal plane positions. GIS detector images from these observations with the corrected attitude, in 10 energy intervals for each pointing, are available via anonymous ftp from

ftp.astro.isas.ac.jp: /asca/calibration/xrt/data/image/*

together with a README file which has more details. Table 1 lists focal plane coordinates sampled by these observations. Figure 4 schematically shows these positions and those for which the PSF can be modeled assuming the mirror symmetry. A star tracker accident occurred during the November 1994 run, but it was possible to restore the images from the affected observations without any loss of quality, tracking the satellite motion using Cyg X-1 itself. The result of this accident is that the PSF we have from the images corresponds to positions averaged over a few-arcmin region of the focal plane due to the source motion in the detector coordinates, for the pointings for which a range of coordinates is given in Table 1. This should have a negligible effect on the results comparing to other uncertainties.

The work is underway to tune the raytracing to reproduce the obtained Cyg X-1 images. In the meantime, a reasonable approximation of the PSF at any focal plane position and energy can be obtained by direct interpolation between these images, assuming that the four mirrors are identical and symmetric. A fortran function make_psf.f which linearly interpolates between these Cyg X-1 images and outputs a 1'-resolution PSF model image for a given energy and focal plane position is available at

ftp.astro.isas.ac.jp: /asca/calibration/xrt/data/make_psf/*

together with the dataset it reads. The limitations and the systematic errors introduced by this method of modeling the PSF are described below.

*Pointing 1, GIS2 observation was divided into 2 pieces with the average phi around 90deg. and 180deg. and the rest was excluded.

Figure 4: Sampled points of the focal plane. The center of the figure corresponds to theta=0, and phi is calculated from the det x axis counterclockwise looking up. Filled symbols represent actual Cyg X-1 positions in the GIS2 and GIS3 images. Using symmetries, the whole usable GIS FOV is covered (open circles), with the off-axis distance increment of about 3-5' and the position angle increment of about 30deg.

Limitations of the PSF model based on Cyg X-1

GIS images of Cyg X-1 are a superposition of the effects of the mirror PSF, the GIS detector PSF, the GIS supporting grid and spacecraft jittering. The procedure used to fix the attitude trouble is applied to all Cyg X-1 pointings, so that the spacecraft jittering is corrected with an accuracy better than that in other observations. A positive effect of this accident is smearing of the supporting grid shadows for most of the pointings. Although the grid shadow is still visible in the Cyg X-1 images, experience shows that ignoring it has a negligible effect on the derived results.

The GIS detector PSF is believed to be a Gaussian independent of the coordinate (although dependent on energy, steeply widening below 2 keV and slightly widening above 8 keV). It has a FWHM of 1' at 2 keV and can be safely ignored when the regions of interest are of several arcminutes in size. For the GIS data analysis, one doesn't have to worry about it at all since it is present in both the data and the PSF model under discussion. However, the SIS detector has no additional blurring and the PSF model we discuss is not directly applicable for SIS analysis. Cyg X-1 is too bright to observe it with SIS. As a temporary solution (before the upgraded raytracing has solved all these problems for good), we suggest modelling the PSF using the GIS Cyg X-1 images which have been smoothed to compensate for the energy dependence of the GIS blurring, and smooth the SIS data to the resolution of the PSF model. There is a non-smoothed set of the Cyg X-1 images for use with the GIS, and a set of images smoothed to the final resolution of Gaussian sigma=0.5' for use with SIS, supplied with the make_psf function. SIS cluster images should be smoothed to the same final resolution sigma=0.5' before collecting the spectra. This can be done by literally smoothing the images in each energy band. Alternatively, without extracting data images in each energy interval, it can be done by smoothing some kind of a mask image applied to the event file when collecting the spectrum of a given region, which before smoothing would consist of 1 and 0 in the pixels inside and outside the region of interest. Work is underway to model the PSF using less bright sources for which the SIS data are available.

In Figure 5, radial brightness profiles of the PSF image generated by interpolation between the Cyg X-1 images are compared with those of 3C273. The profiles are consistent at the energies above 2 keV, but Cyg X-1 always appears to be considerably wider than a point source at the lower energies, which is not an effect of the interpolation nor the mirror asymmetry. The reason is not fully understood at the moment; it may be intrinsic to Cyg X-1 or be connected to its extreme brightness. Therefore, the PSF model based on Cyg X-1 can only be used above 2 keV.

The maximum off-axis distance for which Cyg X-1 images were obtained (and therefore the model under discussion can be used) is 17'. The model ignores the differences between the four mirrors and significant irregularities of each mirror, which introduces a systematic error ~ 5% (sigma) in the predicted flux from a several-arcminute-wide ring centered on the point source. Comparison of the model with the real 2-dimensional images shows that for integration regions other than concentric rings (for example, segments of the ring), the error is greater because of the ignored mirror asymmetries and might be reasonably taken as ~ 15% (1sigma). For a given region, this systematic error should be conservatively assumed the same for all energies (that is, 100% correlated between different energy channels). We recommend avoiding integration regions smaller and rings narrower than a few arcmin.

Poissonian errors in the Cyg X-1 images are generally negligible compared to other errors, but may become significant for small integration regions, far off axis, and at the highest energies because of the poorer statistics.

Extended source analysis

As is mentioned above, PSF scattering has to be taken into account when analyzing extended sources, by simultaneous fitting of the spectra from different image regions. It is implemented in the two ways described below.

1. Method utilizing Monte-Carlo instrument simulator

The ASCA instrument simulator, originally developed for calibration of the detector components of ASCA by the SimASCA working group, has been extensively used to simulate the apparent temperature distribution and brightness profile for clusters of galaxies observed with GIS and SIS (e.g., Ikebe et al. 1995). In the simulator, the XRT PSF is modeled either by interpolating between the Cyg X-1 images or by using the ray-tracing program. In this method, X-ray photons from a model cluster are passed through programs simulating the instruments (XRT, GIS and SIS) to produce a photon list which can be analyzed in exactly the same manner as real data (e.g., using xselect, etc.) The photon list can be compared to the real images or real spectra from different regions and the model parameters can be fit to reproduce the data. The complicated detector characteristics, such as details of the PSF and the pile-up effect of the SIS, can be treated correctly by the Monte-Carlo method. This scheme has been applied to the Centaurus and Fornax clusters by Ikebe (1995) in his PhD thesis, and to A1795 and 3A0336+09 by Ohashi (1995). A sufficient number of model photons, say, 5-10 times more than in the actual data, should be generated so that the statistical fluctuations of the simulated data would not significantly affect the goodness of

the fit between the actual data and the model. The number of photons obtained in a typical cluster observation is 10^5, so that one needs to generate ~10^6 events, which takes a few tens of minutes on an Alpha workstation for one set of the model parameters. Figure 6 shows a simulated brightness distribution (two beta-models), fitted to the GIS image of the Fornax cluster with the galaxy NGC1399.

Figure 5: Comparison of radial brightness profiles of the PSF model based on Cyg X-1 with those of 3C273, for the position theta=4.7' and phi=41deg.. The model is wider at the energies below 2 keV. A similar effect is observed by comparing brightness profiles of Cyg X-1 and another point source observed at the same position with the same detector, therefore, it is not an effect of the interpolation or of the mirror differences.

Figure 6: Simulated image of the Fornax cluster including its cD galaxy NGC 1399, using the Monte-Carlo scheme. The X-ray volume emissivity is modeled as a sum of two beta-models whose parameters are fitted to the actual GIS data (from Ikebe 1995).

2. Generalization of the scheme with telescope ancillary response

Another way is to modify the standard spectral fitting procedure, in which one includes the source geometry and the effective area energy- and position-dependencies in the telescope ancillary response file (ARF), to include the mirror scattering (Markevitch et al. 1995). Denoting a projected sky image of the emission measure of the i-th model region (either two- or three-dimensional) as mi, its spectrum as si(E) (where E is in keV), the total number of the model regions as M, an operation of summing the flux over the j-th detector image region as Rj (including in it the SIS gaps and the GIS grid for clarity), a spectrum from the j-th detector image region as dj(E') (where E' is in channels), the total number of the detector image regions as N, the linear operation of multiplying by the mirror effective area plus PSF scattering, which converts a model brightness distribution into that in the detector plane, as P(E), and convolution of the spectrum with the coordinate-independent detector spectral response including the detector efficiency, as D, we have

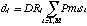
The telescope response transform, , which for a given energy converts the spectra of the model regions to the fluxes in the detector image regions, d = DTs, is thus an M x N matrix that includes the geometry of the source and the integration regions, vignetting and PSF scattering -- an analog of what a commonly used ARF contains, but a matrix instead of a single number. The least-squares solution s is searched by iterations. If there is no PSF scattering and no projection, T is diagonal and everything is reduced to the standard scheme with separate fitting. If mi can be fixed or reasonably simply parametrized (for example, a ROSAT image is available or a symmetric brightness profile can be assumed), T(E) can be calculated once before performing the fit (which involves time-consuming two-dimensional convolutions with the position-dependent PSF), after which only the spectral parameters and maybe relative normalizations of the model spectra need to be fit, each iteration involving only the convolution with the small (for reasonable M and N) matrix T. Figure 7 shows a two-dimensional temperature map of A2319 (Markevitch 1995) obtained using a ROSAT image as a brightness template. In this case, T was a 13 x 13 matrix containing contributions of 13 model regions to the corresponding 13 image regions. To fit a beta-model density profile parameters in addition to the temperatures, one can calculate the transform T for the narrow radial model shells assuming uniform emission measure throughout the cluster, and later recalculate the normalization for each shell in each iteration according to the values of ax and beta, taking advantage of linearity of all the involved operations. Errors in the fitted model parameters may be estimated by Monte-Carlo simulation, adding random deviations to the data and deviations representing systematic errors to the T matrix, and rerunning the fit. Using this scheme on an Alpha workstation, to obtain the temperature map shown in Figure 7 took about 30 min and to calculate errorbars took another day.

For both schemes described above, for evaluation of goodness of the fit, PSF systematic errors may be included in the chi^2 value, for example, by adding 5% or 15% of the model flux (selectively, perhaps only to those components of the model flux which correspond to the non-diagonal elements of T) in quadrature to the statistical error of the data.

Both methods are implemented (although not in the ftools form), and the programs are available from the authors of this article.

Figure 7: Temperature map of A2319, obtained using the modified ARF method (from Markevitch 1995).

References

Ikebe Y., 1995, PhD thesis, Univ. of Tokyo

Ikebe Y., et al., 1995, Hakone ASCA meeting

Ikebe Y., et al., 1995, in preparation

Markevitch, M. 1995, Hakone ASCA meeting

Markevitch, M., et al. 1995, ApJ, in press

Ohashi, T., 1995, Proceedings of the 17th Texas Symposium on Relativistic Astrophysics

Takahashi, T. et al. 1994, "Why we need another Cyg X-1 observation", ASCA internal report, ftp.astro.isas.ac.jp: /asca/report/xrt_US.ps

Proceed to the next article

Return to the previous article

Select another article