ASCA XRT Calibration Issues
K. Gendreau^1, T. Yaqoob^2
1: NASA/GSFC
1 Introduction
We are currently undergoing an extensive recalibration of ASCA. We are updating the physical models of the detectors and mirrors. The main motivation, however, is to resolve discrepancies between the ground and inflight calibration, and to make sure the latter is physically self-consistent. This recalibration effort also takes advantage of the latest knowledge of the mirror response including measurements of the optical constants from AXAF and JET-X.
Part of the motivation is that the physics of the instrument response is just as important as the physics of the sources we are observing, because every photon of information we get from those sources bounces off at least one mirror surface, survives transmission through at least one thermal shield, and must ultimately get detected. The approach taken so far with ASCA has been to introduce "fudge factors'' (Fukazawa et. al. 1997 ASCANEWS Volume 5, 3). These fudge factors are applied to the effective area curves in the interment responses. They are designed to force the instrument to give a nice spectral fit to some astrophysical object. Most users do not see these fudges, but they exist and are large. The include sharp 20-40% spectral features at the Gold M edges, broad band 5-20% continuous changes. Since the fudges are produced from a few observations and since they have no physical basis apart from making those few observations fit, it is quite possible that errors creep in for different situations (e.g. sources at non-standard positions, diffuse sources, time dependent effects, etc...) The fudge factors currently being used in ASCA are shown in figure 1.
In this ASCA News article, we briefly outline issues concerning the mirrors (XRT). We will discuss the optical constants for Gold, uncertainty in the boresight, and several other issues. The discussion is quite brief, due to the limited space here. For more details and many figures see:
http://asd.gsfc.nasa.gov/~kcg/new-asca/cal.html
Figure 1 The arf filter corrections applied to the ASCA response in order to obtain a smooth fit to the Crab and 3C273.
2 Optical Constants
There has been considerable work by several groups on the optical constants used to compute various x-ray properties. For mirrors, reflectivity demands attention be paid to both the real and imaginary components of the optical constants at each energy. For detailed definitions of the optical constants, see any textbook on electromagnetism, or our WWW page. We have looked at 4 sets of optical constants for the ASCA recalibration. We found that the constants used in the release matrices result in several spectral features and that they were inconsistent with Maxwell's Laws.
Our work shows that the constants found by Alan Owens and collaborators are the better choice. Alan Owens kindly provided these constants for our work. The Owens constants (Owens et al , ApJ, 1996, 468, 451) are in good agreement with new values derived by the AXAF transmission grating team currently posted with the new Henke tables available at:
http://www-cxro.lbl.gov/optical_constants/
The Henke Tables are a compilation of X-ray optical constants for all elements.
When computing the reflectivity using these new constants, one must use Gold densities smaller than that of bulk (19.3 g/cm**3). This is due to Gold sputtering effects- the surface is "porous''. AXAF mirror work suggests densities 90% that of Bulk and a similar number was found for BBXRT (ref). Peter Serlimitsos used 88% for BBXRT and for his own ASCA XRT code.
We have computed new ASCA effective area curves for several Gold densities. Here, We simply replace the old optical constant data within the official ASCA XRT raytracing code written by the Nagaza University group. We have taken the new ASCA effective area curves for Gold densities 88% and 90.7% that of bulk Gold, and compared them with the effective areas computed with the Nagoya optical constants. The ratio of the new areas to the old areas is in figure 2:
Figure 2 The Nagoya optical constants vs the new Henke constants
Note the bumps at 2.2 keV and 3.8 keV as well as the hard tails. This alone may explain many of the residuals seen in the ASCA data before released matrices started including fudges of the response by adding 2.2 keV gaussian features. Compare this to figure 2 of Yaqoob et. al. 1994 in PASJ 46 L49.
Of possible concern are the Gold N edges. In particular, the Gold N14 edge at 0.537 keV is very close to the Oxygen edge of the CCD response at 0.532 keV. It is possible that the mirror reflectivity may be smaller here than expected leading to low energy calibration problems. However, there is very little published experimental data on gold optical constants at these energies. We are continuing to work on this area.
3 Optical Axis Uncertainty
Before this recalibration effort, the XRT/GIS teams quoted an uncertainty in their knowledge of the optical boresight position (peak position of the XRT vignetting function) to be +/- 0.5 arcminutes for the GIS. There were no quoted errors for the boresight positions on the SIS detectors. In addition to the quoted errors, there may be further systematic errors since slightly extended sources (the crab nebula and N132D) were used for the boresight determination. An interesting thing to ask is: Given that the XRT boresight has an error of about +/- 0.5 arcminutes, what is the effect on spectral fitting?
To get a handle on this question, we have computed ratios of the Effective Area
vs Energy curves for adjacent off axis angles at a fixed azimuth angle of 45
degrees. Specifically, we look at the effective area curve for  =45
degrees and
=45
degrees and
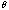 =XX
arcminutes and compare it to the effective area curve for
=XX
arcminutes and compare it to the effective area curve for  =45 degrees and
=45 degrees and
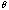 =XX+1
arcminutes. The ratio of these gives you some idea of what the effect of this
uncertainty is on your spectral fitting. Interesting off axis angles to
consider are: 0-1 arcminutes, 5-6 arcminutes, and 8-9 arcminutes. The
"standard" (e.g. 1 CCD mode position) positions are 5-6 arcminutes for some
detectors and 8-9 arcminutes for others.
=XX+1
arcminutes. The ratio of these gives you some idea of what the effect of this
uncertainty is on your spectral fitting. Interesting off axis angles to
consider are: 0-1 arcminutes, 5-6 arcminutes, and 8-9 arcminutes. The
"standard" (e.g. 1 CCD mode position) positions are 5-6 arcminutes for some
detectors and 8-9 arcminutes for others.
These ratios are shown in figure 3.
Figure 3 The theta-ratios
Notice that:
1) even 1 arcminute errors can give 8% uncertainties in normalization
2) 1 arcminute errors can EASILY give you the hard tail seen in the data. But this effect competes with or complements the effects of using the new optical constants.
Given this situation, we have designed a new method to extract the boresights of each of the telescopes. This new method requires a minimum of three observations (4 observations give somewhat more information) of ANY point source(s) at different positions in detector coordinates. The sources may vary with time. Also, we need not know their absolute fluxes. See our WWW page for details on the method.
In the table below, we list our results for the new boresight positions in detector coordinates. In the analysis we could find boresight positions which made the following pairs of sensors agree to a fraction of a percent. Note, that we could not get agreement to better than about 5% for any SIS-GIS pair. This is probably due to some intrinsic instrument calibration problems.
SIS0 to SIS1: Flux Agreement to 0.85%
GIS2 to GIS3: Flux Agreement to 0.85%
________________________________________________________________________________ Sensor X Y Delta From Current Release ________________________________________________________________________________ SIS-S0 675 595 1.03 mm SIS-S1 632.5 790 0.58 mm GIS-S2 132.25 132.0 0.32 mm GIS-S3 120.25 133.0 0.42 mm ________________________________________________________________________________
The errors from this method are about +/- 0.15 arcminutes. The method also seems to be fairly insensitive to the details of the optical constants used in the XRT response. On our WWW page listed above, we provide a simple script for people to change the boresight assumptions made for their spectra.
Something which may need to be done in the future is to consider the possibility that there are different boresight positions (and focal lengths) for each of the 14 sectors within an XRT quadrant. The working model here, is that the sectors are defined by comb-like alignment bars which define the radii of curvature for all the foils azimuthally. If these comb alignment bars shifted during launch, then distinct features would appear in the PSF and different sectors would have different focal points.
4 Wandering of Satellite
The concept behind inaccurrate boresight knowledge lends itself it a number of similar problems. This include wandering of the satellite during an observation and finite source size approximations (e.g. 1-3 arcminute wide sources approximated as point sources).
Given our sensetivity to the position of the boresight (shown above), if the satellite wanders during an observation by a few tenths of an arcminute, then there will be errors in the assumed response, if a single spectra and one fixed boresight ARF is assumed. In addition to telescope issues described above, there are more complications when one considers the GIS window grids and possible gain map uncertainties.
As an example, consider the figure below which indicates the typical pointing positions during the long observation of the crab made on September 28, 1994.
Figure 4 The jitter in the Crab pointing
Looking at figure 5 and figure 3, you might imagine how much distortion there would be in the crab spectrum.
For this long crab pointing, we divided the data based on the RA, and DEC pointing information in the MKF files. We extracted spectra for the different event files and then compared the spectra. Notice that the source is the same and we are actually looking at how the nature of the data changes; no response models are assumed. The ratio of the extracted spectra for two different regions of pointing space are shown in figure 5.
Figure 5 The ratio of the Crab spectra for two different pointings.
A comparison of figure 5 and figure 3 indicates that there is something more complicated going on than mere telescope problems. Notice that in these two graphs, there is a bump at around channel 475- roughly near the Xenon L edges. This may indicate an error in the linearization of the pulseheights.
What is dangerous is that it was this crab pointing which was used to make the "ARFFILTER". The ARFFILTER is the energy dependent fudge factor introduced by the GIS team to force the GIS crab spectrum to a particular power law (see figure 1). Later on, this effect propogates to the SIS during the forced cross calibration of the SIS and GIS during the 3c273 observations.
5 The effects of the finite crab size
On a related issue to telescope wandering and boresight uncertainty, we present here some concerns and analysis of the effects of a finite sized crab nebula when one assumes it is a point source.
Since the Crab is actually about 3 arcminutes across and not a point source, its use as a calibrator with conical mirrors is somewhat compromised. Again, keep in mind that the crab observation discussed in the previous section was used to determine the inflight calibration. We have simulated two possible crab distributions: a uniform brightness 3 arcminute disk and a disk which falls like 1/r to a cut off radius of 3 arcminutes. These simulations were done for the crab at 5 arcminutes off axis. The simulations included full propogation through the XRT raytracing code. Next a standard point source response for the central position was used to produce a ratio of the extended response to the point source response. In both the extended and point source response, the new optical constants were used. The results are in Figure 6.
Figure 6 The ratio of the effective area for 3 arcmin extended objects to point sources.
Note that there are wiggles of the same order of size as the arffilter fudge. The wiggles are at different energies, but recall that the crab distribution is not quite circular and may have an energy dependent figure.
6 Current Status of Recalibration
We have investigated new optical constants and are releasing to the instrument teams new ASCAARF XRT calibration files appropriate to the Owens constants for the following Gold densities (17.5, 18.0, and 18.5 g/cc).
We have used a new method to redetermine optical boresights. We are in the process of investigating the effects on the predicted PSF. We are also starting an investigation of changing radii of curvature in the foils due to alignment bar shifts. An important finding is that as yet, there is still about a 5% discrepency between SIS and GIS normalizations. This is probably due to some intrinsic detector response errors.
We have also investigated the effects of wandering pointings, extended crab emission. We have demonstrated several dangers with using the crab as an inflight calibrator. There are many other astrophysical reasons to be cautious with the crab- but we do not address them here.
We now wait for an evaluation from the instrument teams. Our initial analysis of the SIS data is promising though. With the new optical constants and no fudges, the spectral fits with the SIS data to 3c273 data are yield lower chi squares than one gets using the standard released XRT response files- with the fudges applied.
It is expected that in April of 1997, new calibration files will be released to the general observer. However, more refined calibrations will be released in the summer of 1997.
Full details can be found on the recalibration WWW page.
 Proceed to the next article
Proceed to the next article
 Return to the previous article
Return to the previous article


 Select another article
Select another article