|
|
NOTICE:
This Legacy journal article was published in Volume 3, May 1993, and has not been
updated since publication. Please use the search facility above to find regularly-updated information about
this topic elsewhere on the HEASARC site.
|
The Mewe et al. Plasma Emission Code
Jelle S. Kaastra, Rolf Mewe
SRON Leiden & Utrecht
(Space Research Organization Netherlands)
1. Introduction
During the past decades, a sequence of X-ray missions with ever increasing
sensitivity and spectral and spatial resolution has been launched. These
missions showed in many cases the existence of thermal X-ray radiation from hot
astrophysical plasmas for a broad class of astrophysical sources (e.g. solar
and stellar flares, solar and stellar coronae, hot components of the
intragalactic medium, supernova remnants, clusters of galaxies, etc.).
Motivated by these observations, several computer codes have been developed in
the past in order to explain the observed X-ray emission and to understand the
physics of the emitting objects. A review and short discussion on many of these
models was given by Drake (1992). In this contribution we will focus our
attention to the code of Mewe et al. After giving a short historical
overview on the development of this code, we will discuss the currently
available code. We will give a few examples on the use of it. Finally, we
discuss the future developments of the code.
2. Historical background: the 1985 code
Starting in the early seventies, R. Mewe (1972, 1975, Papers I & II) and
collaborators at SRON-Utrecht and SRON-Leiden developed a scientific
computational package for the calculation of X-ray spectra from hot,
optically-thin plasmas. Its scope was to determine the physical parameters of
hot astrophysical and laboratory plasmas and to compare them with astronomical
space-based observations. The final stage of the software is often called the
Mewe-Gronenschild-van den Oord code. It is essentially based upon the work of
Mewe and Gronenschild (1981, Paper IV) and Mewe, Gronenschild & van den
Oord (1985, Paper V) for the line emission and includes 2167 lines from 15
different chemical elements, covering the wavelength region 1-300 Å.
These lines are produced by excitation from electron impact, radiative and
dielectronic recombination and by innershell excitation and ionization. In
addition to the lines the code calculated the contributions from continuum
radiation due to free-free, free-bound, and two-photon emission following
Gronenschild and Mewe (1978, Paper III), Mewe, Lemen & van den Oord (1986,
Paper VI).
This code has been applied on many occasions to optically thin plasmas, both in
steady-state equilibrium (e.g. stellar coronae) and for a time-dependent
ionization balance (e.g. supernova remnants).
The code allows the user to vary several quantities independently, such as the
electron temperature, electron density, elemental abundances and, for a few
helium-like spectral lines, the incoming, diluted blackbody radiation field.
The collisional ionization equilibrium version of this code has been used to
construct table models for XSPEC and is available (for a restricted set of free
parameters, however) as the XSPEC model `Mewe'.
3. Recent developments: the 1992 code
In the last five years many improvements and extensions to the 1985 code have
been made. First, the structure of the subroutines has been changed, sometimes
drastically, in order to allow all input/output variables to be transmitted as
subroutine arguments. Due to historical reasons, this was not always the case
in the 1985 code. Further, the speed of the code has been increased
significantly by several optimizations, and many improvements and extensions in
the modeling of the physical processes have been made.
3.1. Ionization balance
The transition rates (direct ionization, excitation-autoionization, radiative
recombination and dielectronic recombination) are now taken from the work of
Arnaud & Rothenflug (1985). These transition rates, in general, agree well
with laboratory experiments; however sometimes deviations of 10 % occur at
particular energies. Another approximate estimate of the systematic
uncertainties present in the transition rates can be made by comparing the
results obtained by using the transition rates as given in paper IV, for
example. The resulting equilibrium population of the ionization states
obtained by using the respective sets of transition rates are always consistent
to within 20 %.
In the ionization balance as well as in the spectral calculations, all ions of
the 15 most important chemical elements are included: H, He, C, N, O, Ne, Na,
Mg, Al, Si, S, Ar, Ca, Fe and Ni. As the "standard" abundances we adopt the
recent compilation by Anders & Grevesse (1989) as listed in Table 1.
The speed of the computations of the ionization balance in non-equilibrium
ionization situations was also enhanced significantly, e.g. by replacing the
fourth-order Runge-Kutta scheme to solve the coupled system of first-order
differential rate equations by a matrix inversion; for details see e.g. Jansen
(1988) and Kaastra & Jansen (1993).
Table 1
Element Abundance
H 1
He .0977
C 3.63 x 10-4
N 1.12 x 10-4
O 8.51 x 10-4
Ne 1.23 x 10-4
Na 2.14 x 10-6
Mg 3.80 x 10-5
Al 2.95 x 10-6
Si 3.55 x 10-5
S 1.62 x 10-5
Ar 3.63 x 10-6
Ca 2.29 x 10-6
Fe 4.68 x 10-5
Ni 1.78 x 10-6
3.2. Continuum emission
As soon as the ion concentrations are known it is possible to calculate the
X-ray spectrum, consisting of continuum and line emission. The continuum
emission was described by Mewe and Gronenschild (1978) and Mewe, Lemen &
Van den Oord (1986, Paper VI), and consists of free-free emission, free-bound
emission and two-photon emission.
Paper VI used an approximate formula for the free-free Gaunt factor based upon
a correction to the non-relativistic Born approximation. Since this requires
the evaluation of modified Bessel functions for each energy at which the
spectrum is calculated and for each ion present, the total amount of CPU time
required becomes large for systems such as a supernova remnant with many
shells. Therefore, Kaastra (1992) applied the exact Gaunt factors as calculated
first by Karzas & Latter (1961) and tabulated on a two dimensional grid by
Carson (1988), and interpolated bilinearly and logarithmically on Carson's
grid. This yields the true Gaunt factor within 1%. A relativistic correction at
high temperatures and energies was also applied (equation B4 of Kylafis &
Lamb, 1982).
In paper VI the free-bound Gaunt factor was approximated by assuming that the
individual Gaunt factors for each excited state with principal quantum number n
did not depend upon energy, and that the edge energies of the higher excited
states are equal to the edge energy of the first excited state. In the new code
we take into account the full energy dependence of these partial Gaunt factors
and the correct edge energies of the excited states in the hydrogenic
approximation, using a fit to the tabulated Gaunt factors of Karzas &
Latter (1961).
We did not use the square root of a cosine (paper III) for the two-photon
emission Gaunt factor. Instead, we adopted the more exact values derived from
Spitzer & Greenstein (1961) for hydrogenic ions, and Dalgarno & Drake
(1969) for the helium-like ions.
3.3 Line emission
The 1985 code included 2167 lines of the 15 elements mentioned before, produced
by excitation, radiative recombination, dielectronic recombination and
innershell ionization.
The 1992 code now consists of 2409 lines. Additions originate from the
splitting of some lines into doublets (Lyman alpha, for instance) and the
addition of about 250 dielectronic recombination and innershell excitation
satellite lines of the helium- and hydrogen-like resonance lines from Fe and Ca
between 4-7 keV. For several lines (e.g. helium-like lines from C V to S XV and
lines from Fe IX-XIV, Fe XVIII-XXIII, cf. Mewe et al. 1991), the electron
density dependence is taken into account. In a few cases we slightly changed
the energies of a number of lines around 1 keV, based on a comparison with
measurements of the Flat Crystal Spectrometer on the Solar Maximum Mission (K.
T. Strong, private communication).
4. Applications of the 1992 code: XSPEC model MEKA (Mewe-Kaastra)
The collisional-equilibrium emission code has been installed as an XSPEC model
in the latest release of XSPEC (version 8.23). The model is called MEKA. Free
parameters are the electron temperature (keV), the Hydrogen density (cm-3)
and the abundances of 14 elements from He to Ni. The abundances are defined
with respect to the standard solar abundances mentioned in section 3.1. Note
that in this definition Hydrogen has always abundance 1, and therefore the
Hydrogen abundance is not a free parameter. The normalization of the model is
the quantity A, defined by
A = ne V / (nH d2) (1)
in units of
1050 cm3 pc-2 (=1.0503 x 1011 m)
where ne and nH are the electron and Hydrogen density
of the plasma, d the distance to the source and V the volume of the source.
Since one of the other input variables is the Hydrogen density,
the usual reduced emission measure C as used in the 1985 code is
C = ne2 V / d2 = A nH2 f, (2)
where
f = ne / nH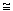 1 +
2nHe 1 +
2nHe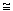 1.2
for the abundances used here. Note that we defined C in such a way that it
contains d2
and not 4 1.2
for the abundances used here. Note that we defined C in such a way that it
contains d2
and not 4  d2 d2
The model is valid for temperatures in the range of about
104 K to 1010 K.
At low temperatures, the plasma becomes nearly neutral and then effects of
charge transfer reactions (not included in the code) alter the ionization
balance; at extreme high temperatures the relativistic corrections become too
large. Correspondingly, the valid energy range for the code is for the
continuum 0-~500 keV; for the lines the valid energy range is 0.041-10 keV. (At
higher energies, there are no lines; at lower energies, we did not include
lines.) The density range is typically from 0 to 1014 cm-3,
depending slightly upon the transition; in our code we assume that the
population of excited atomic levels is negligible. Also we are in the optically
thin limit, i.e. no photo-ionization or photo-excitation effects are taken
into account.
As an example we show below a simulation of the spectrum of AR Lac, with the
parameters adopted from a two-temperature fit to SSS data with a Raymond-Smith
(1977) spectrum made by Drake et al. (1992). The simulation is done for the
planned XMM reflection grating spectrometer (XMM-RGS) and use is made of the
fake-option of XSPEC. An integration time of 10000 s was used. Figure 1 shows
a part of the spectrum near the Fe-L complex, between 0.8 and 1.2 keV. Many
spectral lines are visible. Figure 2 shows the model spectrum of the soft
component only. Many spectral lines and the free-bound emission edge of O VIII
near 0.87 keV are clearly visible.
Fig. 1. Simulation of an XMM-RGS spectrum of AR
Lac for 104 s
integration time with parameters adopted from Drake et al. (1992).
Fig 2. The soft X-ray model component only of the
spectrum shown in Fig. 1.
5. Future developments: SPEX
The 1992 code presented here is an end-product. We do not intend to extend or
improve it further, since we have started work on a code with a completely new
design and much more powerful application possibilities: the SPEctral X-ray and
UV modeling and analysis package (SPEX) is now under development at
SRON-Utrecht and at SRON-Leiden.
Scope of the new work is to include a wide range of astrophysical situations
which can be analyzed with one software package.
Current and future developments are pointed to extend the work to nebular-type,
photo-ionized plasmas (cf. Kaastra and Mewe, 1992a,b). This will be needed
since it has become evident that photo-ionized plasmas play an important role
in accretion-powered X-ray sources (X-ray binaries, cataclysmic variables, and
active galactic nuclei) where a central X-ray emitting region is surrounded by
a cooler, partially ionized medium, and in early-type stars where X-rays
produced in shocks are transferred through a stellar wind.
Moreover, atomic physics has improved considerably during the last decade, and
the advent of a new series of satellites with high sensitivity and spectral
resolution like EUVE, ASCA, SAX, AXAF, and XMM strongly demand the availability
of spectral codes with higher accuracy and more detail.
SPEX will encompass a number of subroutines for the computation of emergent
spectra of optically thin plasmas such as stellar coronal loop structures and
supernova remnants (also including transient ionization effects), as well as
photo-ionized and optically thick plasmas.
A spectral fitting mode and a subroutine for Differential Emission Measure
modeling will also become available. Depending on the various applications to
possible source configurations we will deal with a number of cases, such as:
- Multi-temperature plasma (optically thin, steady state, Differential Emission
Measure (DEM) modeling)
- SuperNova Remnants (SNR) (optically thin, multi-temperature structure,
transient state)
- Solar flare plasma (optically thin, transient state)
- Active Region Loop Spectrum (ARLS) (optically thin, multi-temperature
structure, steady state)
- Photo-ionized plasma (nebular type)
At the moment, updating the atomic physics is in progress. The current
experimental version of SPEX now contains nearly 2800 spectral lines between
1-2000 Å. About 300 far UV lines between from the work of Landini and
Monsignori Fossi (1990) and about 60 dielectronic recombination lines to the
helium-like Mg lines at 1.3 keV have been included.
Several dielectronic and innershell excitation satellite lines which were
lumped together in the 1985 and 1992 code are split now in the new code and
more than 1000 dielectronic recombination (DR) satellite lines and 400 K-alpha
and K-beta lines between 0.3 and 10 keV will be inserted. A major revision of
the atomic data parameters and line wavelengths has been started now on the
basis of a search through the literature on excitation cross sections and
spectral line compilations. After completing the H- to Be-iso-electronic
sequences (including the element P with abundance 2.82 x 10-7)
and inserting the DR lines, the database will contain more than 5000 lines from
16 elements. Moreover, all ions of the 14 cosmically less abundant elements
with atomic number Z < 31 will be included to complete the 16 elements in
the current code.
Some preliminary results obtained with the code extended by Kaastra towards
photo-ionized plasmas have been presented by Mewe (1992), but this part of the
code is still under development.
At the moment, various documents are in preparation in order to give a detailed
description of the software package SPEX including the physical background and
examples of results of spectral calculations.
It is our intention that older versions of SPEX will be continuously updated
and collected into an increasingly more complete package and maintained in
order to reflect the state of the art on X-ray and UV spectral modeling. All
software is completely documented. At the moment we are investigating the
possibilities and conditions for future distribution of the new code.
References
Anders, E., Grevesse, N., 1989, Geochimica et Cosmochimica Acta
53, 197
Arnaud, M., Rothenflug, R., 1985, Astr. Ap. Supp. 60, 425.
Carson, T.R., 1988, Astr. Ap. 189, 319.
Dalgarno, A., Drake, G.W.F., 1979, Les Congrès et Colloques de
l'Université de Liège, Belgium, Vol. 54, p.69.
Drake, S.A., 1992, Legacy 1, 59.
Drake, S.A., Arnaud, K.A., White, N., 1992, Legacy 1, 43.
Gronenschild, E.H.B.M., Mewe, R., 1978, Astr. Ap. Supp. 32, 283
(Paper III).
Jansen, F.A., 1988, Ph. D. Thesis, Leiden University.
Kaastra, J.S.: 1992, An X-ray spectral code for optically thin plasmas,
internal SRON-Leiden Report, updated version 2.0 dd. 12-03-1992.
Kaastra, J.S., Jansen, F.A.: 1993 Astr. Ap., in press.
Kaastra, J.S., Mewe, R., 1993a, Astr. Ap. Supp. 97, 443.
Kaastra, J.S., Mewe, R., 1993b in Proc. 10th Int. Colloquium on UV and X-ray
spectroscopy of astrophysical and laboratory plasmas, eds. E.H. Silver and
S.M. Kahn, Cambridge Univ. Press, in press.
Karzas, W.J., Latter, R., 1961, Ap. J. Supp. 6, 167.
Kylafis, N.D., Lamb, D.Q., 1982, Ap. J. Supp. 48, 239.
Landini, M., Monsignori Fossi, B.C., 1990, Astr. Ap. Supp. 82,
229.
Mewe, R.: 1972, Solar Phys. 22, 459 (Paper I).
Mewe, R.: 1975, Solar Phys. 44, 383 (Paper II).
Mewe, R.: 1992, in Proc. Workshop of UK SERC's Collaborative Computational
Project No 7 (CCP7) on The physics of chromospheres, coronae and winds, eds.
C.S. Jeffery and R.E.M. Griffin, Cambridge University Printing Service, p.
33.
Mewe, R., Gronenschild, E.H.B.M., 1981, Astr. Ap. Supp. 45, 11
(Paper IV).
Mewe, R., Gronenschild, E.H.B.M., van den Oord, G.H.J., 1985, Astr. Ap.
Supp. 62, 197 (Paper V).
Mewe, R., Lemen, J.R., van den Oord, G.H.J., 1986, Astr. Ap. Supp.
65, 511 (Paper VI).
Mewe, R., Lemen, J.R., Schrijver, C..J., 1991, Ap. Space Sci.
182, 35.
Karzas, W.J., Latter, R.; 1961; Ap. J. Supp. 6, 167.
Raymond, J.C., Smith, B.W., 1977, Ap. J. Supp. 35, 419.
Spitzer, L., Greenstein, J.L., 1951, Ap. J. 114, 407.
 Proceed to the next article
Proceed to the next article
 Return to the previous article
Return to the previous article
 Select another article
Select another article
HEASARC Home |
Observatories |
Archive |
Calibration |
Software |
Tools |
Students/Teachers/Public
Last modified: Monday, 19-Jun-2006 11:40:52 EDT
|