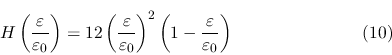Next: Continuum Opacity and Thomson Up: Recombination Continuum Emission and Previous: Line Emission and Escape Contents
Diffuse continuum radiation is emitted by three processes: thermal bremsstrahlung, radiative recombination, and two-photon decays of metastable levels. The thermal bremsstrahlung emissivity is given by [Osterbrock 1974]:
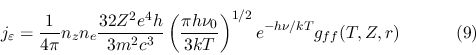
where T is the electron temperature, ![]() is the electron abundance, Z is the charge on the most abundant ion,
is the electron abundance, Z is the charge on the most abundant ion,
![]() is the abundance of that ion, and
is the abundance of that ion, and ![]() is a Gaunt
factor ([Karzas and Latter, 1966]). For two photon decays, we adopt the
distribution ([Tucker and Koren 1971]):
is a Gaunt
factor ([Karzas and Latter, 1966]). For two photon decays, we adopt the
distribution ([Tucker and Koren 1971]):