Next: bknpower, zbknpower: broken power Up: Additive Model Components Previous: bexriv: reflected e-folded broken
A three-segment broken power law (i.e. with two break energies).
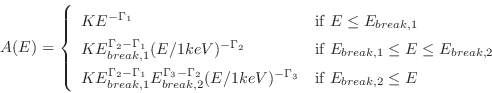
where:
| par1 = |
power law photon index for
|
| par2 = |
first break point for the energy in keV |
| par3 = |
power law photon index for
|
| par4 = |
second break point for the energy in keV |
| par5 = |
power law photon index for
|
| norm = K | photons/keV/cm |
If POW_EMIN and POW_EMAX have been defined by the xset command then
the norm becomes the flux in units of ![]() ergs/cm
ergs/cm![]() /s over the
energy range (POW_EMIN, POW_EMAX) keV unless POW_EMIN = POW_EMAX in
which case the norm becomes the flux density in micro-Jansky at
POW_EMIN keV. In these cases it is important that POW_EMIN and
POW_EMAX lie within the energy range on which the model is being
evaluated.
/s over the
energy range (POW_EMIN, POW_EMAX) keV unless POW_EMIN = POW_EMAX in
which case the norm becomes the flux density in micro-Jansky at
POW_EMIN keV. In these cases it is important that POW_EMIN and
POW_EMAX lie within the energy range on which the model is being
evaluated.