Next: 3.4.2 RFC chip arrays Up: 3.4 REFLECTION GRATING SPECTROMETER (RGS) Previous: 3.4 REFLECTION GRATING SPECTROMETER (RGS)
The diffraction geometry of the reflection gratings is illustrated in
Fig. 76. Light strikes the gratings at an angle of
incidence 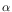 with respect to the plane of the grating, and emerges
at angle
with respect to the plane of the grating, and emerges
at angle 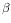 given by the dispersion equation
given by the dispersion equation
where 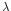 is the radiation wavelength, d the grating
spacing, and m the spectral order. The RGS is designed for use with
negative orders,
is the radiation wavelength, d the grating
spacing, and m the spectral order. The RGS is designed for use with
negative orders,
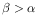 .
.