Next: Appendix C: Adding Models Up: XspecManual Previous: Appendix A: The User
Introduction
There are two operations performed in XSPEC that require statistics. The first is parameter estimation, which comprises finding the parameters for a given model that provide the best fit to the data and then estimating uncertainties on these parameters. The second operation is testing whether the model and its best-fit parameters actually match the data. This is usually referred to as determining the goodness-of-fit.
Which statistics should be used for these two operations depends on the probability distributions underlying the data. Almost all astronomical data are drawn from one of two distributions: Gaussian (or normal) and Poisson. The Poisson distribution is the familiar case of counting statistics and is valid whenever the only source of experimental noise is due to the number of events arriving at the detector. This is a good approximation for modern CCD instruments. If some other sort of noise is dominant then it is usually described by the Gaussian distribution. A common example of this is detectors that require background to be modeled in some way, rather than directly measured. The uncertainty in the background modeling is assumed to be Gaussian.
In the limit of large numbers of counts the Poisson distribution can be well approximated by a Gaussian so the latter is often used for detectors with high counting rates. In most cases this will cause no errors and does simplify the handling of background uncertainties however care should be exercised that no systematic offsets are introduced.
A fuller discussion of many of the issues discussed in this appendix can be found in Siemiginowska (2011).
Parameter Estimation
The standard statistic used in parameter estimation is the maximum likelihood. This is based on the intuitive idea that the best values of the parameters are those that maximize the probability of the observed data given the model. The likelihood is defined as the total probability of observing the data given the model and current parameters. In practice, the statistic used is twice the negative log likelihood.
Gaussian data (chi)
The likelihood for Gaussian data is
![\begin{displaymath}
L = \prod_{i=1}^N {1\over{\sigma_i\sqrt{2\pi}}}
\exp\left[{{-(y_i-m_i)^2\over{2\sigma_i^2}}}\right]
\end{displaymath}](img521.png) |
(B.1) |
where ![]() are the observed data rates,
are the observed data rates, ![]() their errors, and
their errors, and ![]() the
values of the predicted data rates based on the model (with current
parameters) and instrumental response. Taking twice the negative
natural log of L and ignoring terms which depend only on the data (and
will thus not change as parameters are varied) gives the familiar
statistic :
the
values of the predicted data rates based on the model (with current
parameters) and instrumental response. Taking twice the negative
natural log of L and ignoring terms which depend only on the data (and
will thus not change as parameters are varied) gives the familiar
statistic :
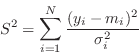 |
(B.2) |
commonly referred to as ![]() and used for the statistic chi option.
and used for the statistic chi option.
Gaussian data with background (chi)
The previous section assumed that the only contribution to the
observed data was from the model. In practice, there is usually
background. This can either be included in the model or taken from
another spectrum file (read in using the back command). In the latter
case the ![]() become observed data rates from the source spectrum
subtracted by the background spectrum and the
become observed data rates from the source spectrum
subtracted by the background spectrum and the ![]() are the source and
background errors added in quadrature. Since the difference of two
Gaussians variables is another Gaussian variable, the
are the source and
background errors added in quadrature. Since the difference of two
Gaussians variables is another Gaussian variable, the ![]() statistic can
still be used in this case.
statistic can
still be used in this case.
Poisson data (cstat)
The likelihood for Poisson distributed data is:
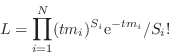 |
(B.3) |
where ![]() are the observed counts,
are the observed counts, ![]() the exposure time, and
the exposure time, and ![]() the predicted count rates based on the current model and instrumental
response. The maximum likelihood-based statistic for Poisson data,
given in Cash (1979), is :
the predicted count rates based on the current model and instrumental
response. The maximum likelihood-based statistic for Poisson data,
given in Cash (1979), is :
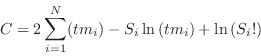 |
(B.4) |
The final term depends only on the data (and hence makes no difference to the best-fit parameters) so can be replaced by Stirling's approximation to give :
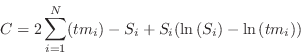 |
(B.5) |
which provides a statistic which asymptotes to ![]() in the limit of large
number of counts (Castor, priv. comm.). This is what is used for the
statistic cstat option. Note that using the
in the limit of large
number of counts (Castor, priv. comm.). This is what is used for the
statistic cstat option. Note that using the ![]() statistic
instead of
statistic
instead of ![]() is not recommended since it can produce biassed results
even when the number of counts is quite large (see
e.g. Humphrey et al. 2009).
is not recommended since it can produce biassed results
even when the number of counts is quite large (see
e.g. Humphrey et al. 2009).
If the statistic is specified as cstatN where N is an integer then the same formula is used except that the data and model are binned so that there are at least N counts in each bin. In general, this is not recommended since it is inefficient but can be useful when testing using simulations.
Poisson data with Poisson background (cstat)
This case is more difficult than that of Gaussian data because the difference between two Poisson variables is not another Poisson variable so the background data cannot be subtracted from the source and used within the C statistic. The combined likelihood for the source and background observations can be written as:
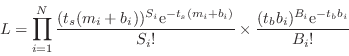 |
(B.6) |
where ![]() and
and ![]() are the exposure times for the source and
background spectra, respectively,
are the exposure times for the source and
background spectra, respectively, ![]() are the background data and
are the background data and ![]() the predicted rates from a model for the expected background. Note
that
the predicted rates from a model for the expected background. Note
that ![]() is the predicted background rate for the observation of the
source. If the background is uniform and the source and background
observations are extracted from different sized regions then
is the predicted background rate for the observation of the
source. If the background is uniform and the source and background
observations are extracted from different sized regions then ![]() should be the background observation exposure multiplied by the the
ratio of the background to source region sizes. If there
is a physically motivated model for the background then this
likelihood can be used to derive a statistic which can be minimized
while varying the parameters for both the source and background
models.
should be the background observation exposure multiplied by the the
ratio of the background to source region sizes. If there
is a physically motivated model for the background then this
likelihood can be used to derive a statistic which can be minimized
while varying the parameters for both the source and background
models.
As a simple illustration suppose the source spectrum is source.pha and the background spectrum back.pha. The source model is an absorbed apec and the background model is a power-law. Further suppose that the background model requires a different response matrix to the source, backmod.rsp say. The fit is set up by:
XSPEC12> data 1:1 source.pha 2:2 background.pha XSPEC12> resp 2:1 backmod.rsp 2:2 backmod.rsp XSPEC12> model phabs(apec) XSPEC12> model 2:backmodel pow
where the normalization of the apec model is fixed to zero for the second data group (i.e. the background spectrum) and the parameters of the background model are linked between the data groups.
If there is no appropriate model for the background it is still
possible to proceed. Suppose that each bin in the background spectrum
is given its own parameter so that the background model is ![]() . A
standard XSPEC fit for all these parameters would be impractical
however there is an analytical solution for the best-fit
. A
standard XSPEC fit for all these parameters would be impractical
however there is an analytical solution for the best-fit ![]() in terms
of the other variables which can be derived by using the fact that the
derivative of
in terms
of the other variables which can be derived by using the fact that the
derivative of ![]() will be zero at the best fit. Solving for the
will be zero at the best fit. Solving for the ![]() and
substituting gives the profile likelihood:
and
substituting gives the profile likelihood:
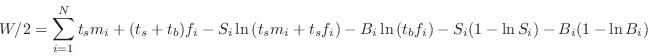 |
(B.7) |
where, if
![]() then
then
| (B.8) |
otherwise
| (B.9) |
and
| (B.10) |
If any bin has ![]() and/or
and/or ![]() zero then its contribution to
zero then its contribution to ![]() (
(![]() ) is calculated
as a special case. So, if
) is calculated
as a special case. So, if ![]() is zero then:
is zero then:
| (B.11) |
If ![]() is zero then there are two special cases. If
is zero then there are two special cases. If
![]() then:
then:
| (B.12) |
otherwise:
| (B.13) |
This W statistic is used for statistic cstat if a background spectrum with Poisson statistics has been read in (note that in the screen output it will still be labeled as C statistic). In practice, it works well for many cases but for weak sources and small numbers of counts in the background spectrum it can generate an obviously wrong best fit. A possible solution is to bin the data to ensure every bin in the background spectrum contains enough counts (see https://giacomov.github.io/Bias-in-profile-poisson-likelihood/).
In the limit of large numbers of counts per spectrum bin a
second-order Taylor expansion shows that ![]() tends to :
tends to :
![\begin{displaymath}
\sum_{i=1}^N\left({[S_i-t_sm_i-t_sf_i]^2\over{t_s(m_i+f_i)}}+{[B_i-t_bf_i]^2\over{t_bf_i}}\right)
\end{displaymath}](img550.png) |
(B.14) |
which is distributed as ![]() with
with
![]() degrees of freedom, where
the model
degrees of freedom, where
the model ![]() has M parameters (include the normalization).
has M parameters (include the normalization).
Poisson data with Gaussian background (pgstat)
Another possible background option is if the background spectrum is not Poisson. For instance, it may have been generated by some model based on correlations between the background counts and spacecraft orbital position. In this case there may be an uncertainty associated with the background which is assumed to be Gaussian. In this case the same technique as above can be used to derive a profile likelihood statistic :
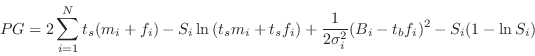 |
(B.15) |
where
| (B.16) |
unless this gives ![]() in which case
in which case
| (B.17) |
and
| (B.18) |
The positive or negative square root is chosen depending on whether
![]() is greater than or less than zero, respectively.
is greater than or less than zero, respectively.
There is a special case for any bin with ![]() equal to zero:
equal to zero:
| (B.19) |
This is what is used for the statistic pgstat option.
Poisson data with known background (pstat)
Another possible background option is if the background spectrum is known. Again the same technique as above can be used to derive a profile likelihood statistic :
![\begin{displaymath}
P = 2\sum_{i=1}^N t_s(m_i+B_i/t_b)-S_i\ln{[t_s(m_i+B_i/t_b]}-S_i(1-\ln{S_i})
\end{displaymath}](img559.png) |
(B.20) |
This is what is used for the statistic pstat option.
Bayesian analysis of Poisson data with Poisson background (lstat)
An alternative approach to fitting Poisson data with background is to use Bayesian methods. In this case instead of solving for the background rate parameters we marginalize over them writing the joint probability distribution of the source parameters as :
| (B.21) |
where ![]() are the source parameters,
are the source parameters, ![]() the
background rate parameters and
the
background rate parameters and ![]() any prior information. Using Bayes
theorem, that the
any prior information. Using Bayes
theorem, that the ![]() and independent of the
and independent of the ![]() , that the
, that the ![]() are
individually independent and that the observed counts are Poisson gives :
are
individually independent and that the observed counts are Poisson gives :
 |
(B.22) |
where :
| (B.23) |
To calculate ![]() we need to make an assumption about the prior
background probability distribution,
we need to make an assumption about the prior
background probability distribution, ![]() . We follow Loredo (1992)
and assume a uniform prior between 0 and
. We follow Loredo (1992)
and assume a uniform prior between 0 and ![]() . Expanding the binomial
gives :
. Expanding the binomial
gives :
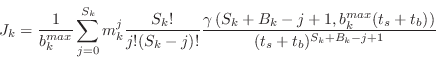 |
(B.24) |
where :
| (B.25) |
Again, following Loredo we assume that
![]() and
using the approximation
and
using the approximation
![]() when
when
![]() gives :
gives :
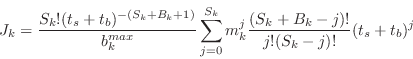 |
(B.26) |
Note that for ![]() only the
only the ![]() term in the summation is
non-zero. Now, we define lstat by calculating
term in the summation is
non-zero. Now, we define lstat by calculating ![]() and ignoring all
additive terms which are independent of the model parameters :
and ignoring all
additive terms which are independent of the model parameters :
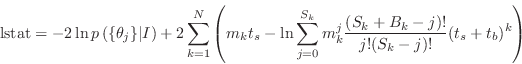 |
(B.27) |
Including Bayesian priors
If Bayesian priors have been set using the bayes command then
![]() is added to the fit statistic
value. The bayes documentation gives
is added to the fit statistic
value. The bayes documentation gives
![]() for each option.
for each option.
Power spectra from time series data (whittle)
XSPEC has been used by a number of researchers to fit models to power spectra from time series data. In this case the x-axis is frequency (in Hz) and not keV so plots have to be modified appropriately. The correct fit statistic is that due to Whittle as discussed in Vaughan (2010) and Barret & Vaughan (2012) :
 |
(B.28) |
Parameter confidence regions
Fisher Matrix
XSPEC provides several different methods to estimate the precision with which parameters are determined. The simplest, and least reliable, is based on the inverse of the second derivative of the statistic with respect to the parameter at the best fit. The first derivative must be zero by construction and the second derivative provides a measure of how rapidly the statistic increases away from the best-fit. The faster the statistic increases, i.e. the larger the second derivative, the more precisely the parameter is determined. The matrix of second derivatives is often referred to as the Fisher information. Its inverse is the covariance matrix, written out at the end of an XSPEC fit.
The +/- numbers provided for each parameter in the standard fit output are estimates of the one-sigma uncertainty, calculated as the square root of the diagonal elements of the covariance matrix. As such, these ignore any correlations between parameters. Whether correlations are important can be seen by comparing with the off-diagonal elements of the covariance matrix. In general, these estimates should be considered lower limits to the true uncertainty.
Correlation information is also given in the table of variances and principal axes which also appears at the end of a fit. Each row in this table is an eigenvalue and associated eigenvector of the Fisher matrix. If the parameters are independent then each eigenvector will have a contribution from only one parameter. For instance, if there are three independent parameters then the eigenvectors will be (1,0,0), (0,1,0), and (0,0,1). If the parameters are not independent then each eigenvector will show contributions from more than one parameter.
Delta Statistic
The next most reliable method for deriving parameter confidence regions is to find surfaces of constant delta statistic from the best-fit value, i.e. where :
| (B.29) |
This is the method used by the error command, which searches for the
parameter value where the statistic differs from that at the best fit
by a value (![]() ) specified in the command. For each value of the
parameter being tested all other free parameters are allowed to
vary. The results of the error command can be checked using steppar,
which can also be used to find simultaneous confidence regions of
multiple parameters. The specific values of
) specified in the command. For each value of the
parameter being tested all other free parameters are allowed to
vary. The results of the error command can be checked using steppar,
which can also be used to find simultaneous confidence regions of
multiple parameters. The specific values of ![]() which generate
particular confidence regions are calculated by assuming that it is
distributed as
which generate
particular confidence regions are calculated by assuming that it is
distributed as ![]() with the number of degrees of freedom equal to the
number of parameters being tested (e.g. when using the error command
there is one degree of freedom, when using steppar for two parameters
followed by plot contour there are two degrees of freedom). This
assumption is correct for the
with the number of degrees of freedom equal to the
number of parameters being tested (e.g. when using the error command
there is one degree of freedom, when using steppar for two parameters
followed by plot contour there are two degrees of freedom). This
assumption is correct for the ![]() statistic and is asymptotically
correct for other statistic choices.
statistic and is asymptotically
correct for other statistic choices.
Monte Carlo
The best but most computationally expensive methods for estimating parameter confidence regions are using two different Monte Carlo techniques. The first technique is to start with the best fit model and parameters and simulate datasets with identical properties (responses, exposure times, etc.) to those observed. For each simulation, perform a fit and record the best-fit parameters. The sets of best-fit parameters now map out the multi-dimensional probability distribution for the parameters assuming that the original best-fit parameters are the true ones. While this is unlikely to be true, the relative distribution should still be accurate so can be used to estimate confidence regions. There is no explicit command in XSPEC to use this technique however it is easy to construct scripts to perform the simulations and store the results.
The second technique is Markov Chain Monte Carlo (MCMC) and is of much wider applicability. In MCMC a chain of sets of parameter values is generated which describe the parameter probability distribution. This determines both the best-fit (the mode) and the confidence regions. The chain command runs MCMC chains which can be converted to probability distributions using margin (which takes the same arguments as steppar). The results can be plotted in 1- or 2-D using plot margin and plot integprob to plot the probability density and integrated probability. If MCMC chains are in use then the error command will use them to estimate the parameter uncertainty.
Goodness-of-fit
Parameter values and confidence regions only mean anything if the
model actual fits the data. The standard way of assessing this is to
perform a test to reject the null hypothesis that the observed data
are drawn from the model. Thus we calculate some statistic ![]() and if
and if
![]() then we reject the model at the confidence
level corresponding to
then we reject the model at the confidence
level corresponding to ![]() . Ideally,
. Ideally, ![]() is
independent of the model so all that is required to evaluate the test
is a table giving
is
independent of the model so all that is required to evaluate the test
is a table giving ![]() values for different confidence
levels. This is the case for
values for different confidence
levels. This is the case for ![]() which is one of the reasons why
it is used so widely. However, for other test statistics this may not
be true and the distribution of
which is one of the reasons why
it is used so widely. However, for other test statistics this may not
be true and the distribution of ![]() must be estimated for the model in
use then the observed value compared to that distribution. This is
done in XSPEC using the goodness command. The model is simulated
many times using parameter values drawn from the posterior probability
distribution, each fake dataset is fit and a value of
must be estimated for the model in
use then the observed value compared to that distribution. This is
done in XSPEC using the goodness command. The model is simulated
many times using parameter values drawn from the posterior probability
distribution, each fake dataset is fit and a value of ![]() calculated. These are then ordered and a distribution
constructed. This distribution can be plotted using plot
goodness. Now suppose that
calculated. These are then ordered and a distribution
constructed. This distribution can be plotted using plot
goodness. Now suppose that ![]() obs exceeds 90% of the
simulated
obs exceeds 90% of the
simulated ![]() values we can reject the model at 90% confidence. For
more discussion about the goodness command see the discussion
on the Facebook xspec group.
values we can reject the model at 90% confidence. For
more discussion about the goodness command see the discussion
on the Facebook xspec group.
It is worth emphasizing that goodness-of-fit testing only allows us to reject a model with a certain level of confidence, it never provides us with a probability that this is the correct model.
Chi-square (chi)
The standard goodness-of-fit test for Gaussian data is ![]() (as defined
above). At the end of a fit, XSPEC writes out the
(as defined
above). At the end of a fit, XSPEC writes out the ![]() and
the number of degrees of freedom (dof = number of data bins minus
number of free parameters). A rough rule of thumb is that the
and
the number of degrees of freedom (dof = number of data bins minus
number of free parameters). A rough rule of thumb is that the ![]() should be approximately equal to the dof. If the
should be approximately equal to the dof. If the ![]() is much greater
than the dof then the observed data are likely not drawn from the
model. If the
is much greater
than the dof then the observed data are likely not drawn from the
model. If the ![]() is much less than the dof then the Gaussian sigma
associated with the data are likely over-estimated. XSPEC also writes
out the null hypothesis probability, which is the probability of the
observed data being drawn from the model given the value of
is much less than the dof then the Gaussian sigma
associated with the data are likely over-estimated. XSPEC also writes
out the null hypothesis probability, which is the probability of the
observed data being drawn from the model given the value of ![]() and the
dof.
and the
dof.
Pearson chi-square (pchi)
Pearson's original (1900) chi-square test was not for Gaussian data but for the case of dividing counts up between cells. This corresponds to the case of Poisson data with no background.
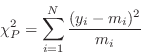 |
(B.30) |
Kolmogorov-Smirnov (ks)
There are a number of test statistics based on the empirical distribution function (EDF). The EDF is the cumulative spectrum :
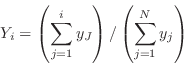 |
(B.31) |
for the data and
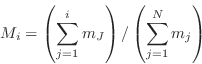 |
(B.32) |
for the model.
The EDF can be plotted using plot icounts. The best known of these tests is Kolmogorov-Smirnov whose statistic is simply the largest difference between the observed and model EDFs :
| (B.33) |
The XSPEC statistic test ks option returns ![]() . The significance of
the ks value can be determined using the goodness command. In
general, the Kolmogorov-Smirnov test is not particularly powerful and
the next two test statistics are preferred.
. The significance of
the ks value can be determined using the goodness command. In
general, the Kolmogorov-Smirnov test is not particularly powerful and
the next two test statistics are preferred.
Cramer-von Mises (cvm)
The Cramer-von Mises statistic is the sum of the squared differences of the EDFs :
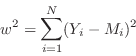 |
(B.34) |
The XSPEC statistic test cvm option returns ![]() and its
significance should be determined using the goodness command.
and its
significance should be determined using the goodness command.
Anderson-Darling (ad)
Anderson-Darling is a modification of Cramer-von Mises which places more weight on the tails of distribution :
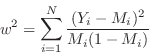 |
(B.35) |
The XSPEC statistic test ad option returns ![]() and its
significance should be determined using the goodness command.
and its
significance should be determined using the goodness command.
CUSUM (cusum)
The CUSUM statistic (Page, E.S. (1954, Biometrika, 41, 100)) is the difference between the largest and smallest differences between the model and data EFS.
| (B.36) |
Runs (runs)
The Runs (or Wald-Wolfowitz) test checks that residuals are randomly
distributed above and below zero and do not cluster. Suppose ![]() is the
number of channels with +ve residuals,
is the
number of channels with +ve residuals, ![]() the number of channels with
negative residuals, and
the number of channels with
negative residuals, and ![]() the number of runs then the Runs statistic
is :
the number of runs then the Runs statistic
is :
| (B.37) |
where :
| (B.38) |
and
| (B.39) |
The hypothesis that the residuals are randomly distributed can be
rejected if abs(Runs) exceeds a critical value. For large sample runs (where
![]() and
and ![]() both exceed 10) the critical value is drawn from the
Normal distribution. For instance, for a test at the 5% significance
level, the hypothesis can be rejected if abs(Runs) exceeds 1.96.
both exceed 10) the critical value is drawn from the
Normal distribution. For instance, for a test at the 5% significance
level, the hypothesis can be rejected if abs(Runs) exceeds 1.96.
References