XMM-Newton
Users Handbook
Several parameters determine the RGS effective area per dispersion
order: the properties of all optical components in the light path, the
CCD quantum efficiency and the source and order filtering criteria.
The following optical components contribute:
- The effective area of the mirror modules (see
§ 3.2.2.1).
- The Reflection Grating Arrays: how much of the light from the
mirrors is diffracted to the different spectral orders and then
absorbed on the RFCs. This is determined by the amount of collimated
light that is intercepted by the grating arrays, the reflectivity of
the gratings into the dispersion order and the effective surface of
the gratings that provides useful dispersed light. Since the gratings
are mounted relatively close together, about 1 cm spacing, light with
large dispersion angles is vignetted by the back of the neighbouring
grating, thus reducing the surface area that provides useful intensity
to the camera at these dispersion angles.
- The quantum efficiency of the RGS focal camera CCDs, which
varies from 70% to 95% over the RGS passband from 0.35 to 2.5 keV.
These three components are functions of wavelength and source position
angle. Finally, data selections in the RFC, used to separate orders and
to suppress scattering, will determine the effective area.
To assess the total efficiency of the RGS instrument per spectral
order, the efficiency with which the background is rejected and the
different spectral orders can be selected must also be taken into
account. This is performed by filtering in the imaging domain
(cross-dispersion versus dispersion angles) and in the domain CCD-PI
versus dispersion angle. Standard data selections are indicated by the
white curves in Fig. 78. In the cross-dispersion
direction a filter is applied which includes typically 95% of the
total intensity. Default masks for the spatial extraction of photons
from the different orders using PHA or PI-energy channel vs. dispersion
coordinate plots, as in Fig. 78, are created by
the offline analysis SAS tasks for each RGS . The user can also
modify the extraction masks as described in the SAS User's Guide. In
addition the exposure time per wavelength bin is calculated taking into
account the data selections, rejected columns and pixels and the dead
space between CCDs. The expected efficiency in the post-observation
RGS order selection with the SAS is about 90% (0.95x0.95). This is
a function of wavelength and is less at shorter wavelengths, due to
additional loss of scatter outside of the extracted (dispersion-PI)
region.
Fig. 84 displays the calculated effective area of
both RGS units together, and Fig. 85 the
individual RGS1 and RGS2 effective areas overlaid one on top of the
other. The calculations have been performed taking into account all the
factors listed above.
Figure 84:
The effective area of both RGS units combined as a
function of energy and wavelength (top and bottom horizontal scales,
respectively). See text for detailed explanations.
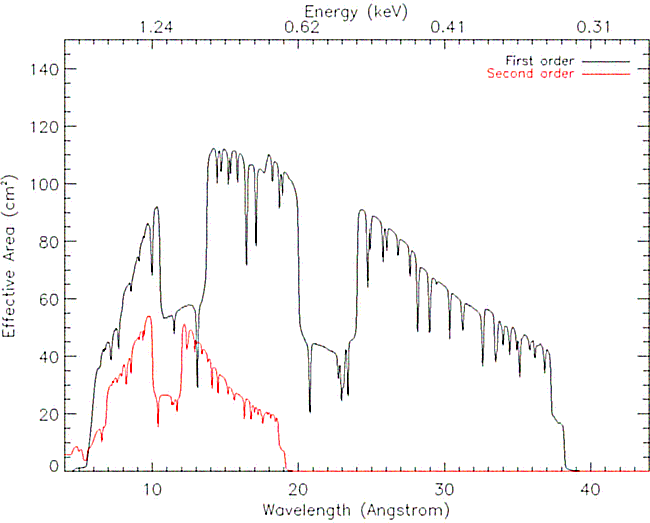 |
Figure 85:
The effective areas of both RGS units separately as a
function of energy and wavelength (top and bottom horizontal scales,
respectively). See text for detailed explanations.
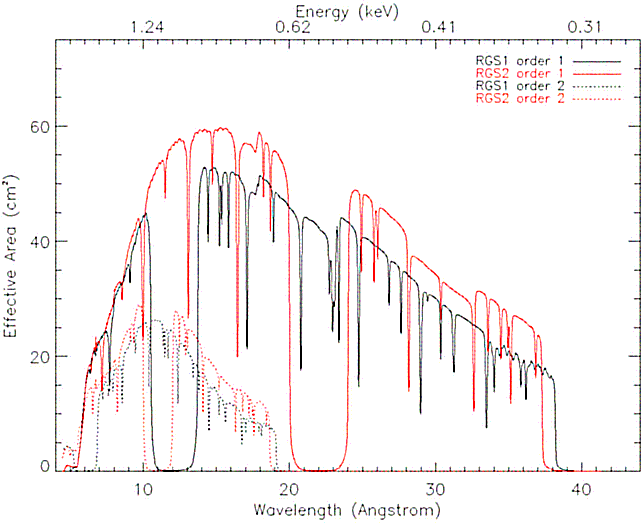 |
Some clear features can be identified from these figures:
- the effective area has broad gaps due to the inoperative CCDs.
- the efficiency around chip boundaries does not drop sharply nor
completely decreases to zero. This is due to the scattering causing
photons with wavelengths corresponding to the passive areas being
redistributed into non-passive areas. The amplitude of this
sensitivity is strongly dependent on the selection mask in CCD PI
versus dispersion coordinate space.
- the total effective area of both RGS added in
Fig. 84 shows several of these chip boundaries,
as the alignment of the RGS cameras is such that the inter-chip gaps
do not coincide in wavelength.
- a similar effect of lower area as with the inter-chip gaps can be
seen at wavelengths equivalent to bad columns, but there it is less
pronounced.
- absorption edges are due to the existence of passive layers in
the X-ray path consisting of the following atoms: Si (6.74 Å), Al
(7.95 Å), Mg (9.51 Å), F (17.80 Å) and O (22.83 Å)
- apparent oscillations with small amplitude of the effective area
are due to data selections by regions that are defined as polygons
across the surface of binned two dimensional data (cross dispersion
versus dispersion angle and CCD energy versus dispersion angle). The
fact that pixels of these binned images are selected discretely, gives
rise to small scale variations of the selected area within the
region. This is seen as oscillations of the detection efficiency.
This is not a problem, nor is it an additional uncertainty of the
response, as these data selection effects are properly included in the
response generation.
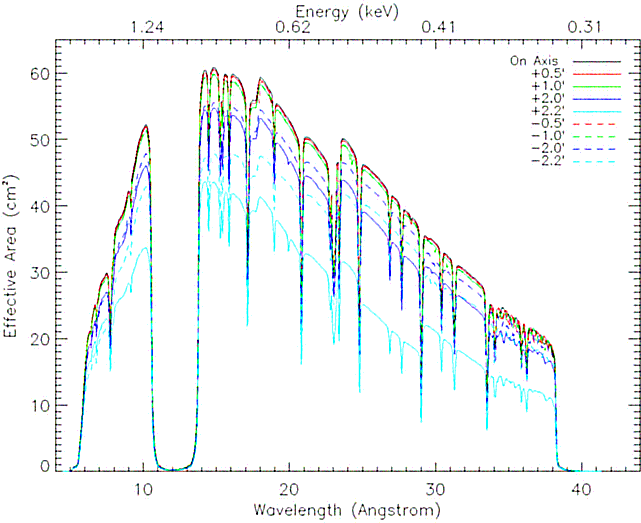
Fig. 86 shows the effective area as a function of the
off-axis cross dispersion angle. The ratio of the median off-axis
effective area to the on-axis values decreases from 0.994 at
 0
0 .5 to 0.83 and 0.60 at -2
.5 to 0.83 and 0.60 at -2 .2 and +2
.2 and +2 .2,
respectively.
.2,
respectively.
Figure 86:
The RGS1 effective area as a function of cross dispersion
off-axis angle.
 |
European Space Agency - XMM-Newton Science Operations Centre


 0
0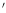 .5 to 0.83 and 0.60 at -2
.5 to 0.83 and 0.60 at -2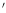 .2 and +2
.2 and +2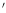 .2,
respectively.
.2,
respectively.