SIS Calibration and Software:
Recent Developments
T. Dotani^1, K. Mitsuda^1, A. Yamashita^1,
H. Ezuka^1, K. Hayashida^2, K. Torii^2, N. Miura^2,
G. Otani^3, C. Crew^4, A. Rasmussen^5,
K. Gendreau^6
1:Institute of Space and Astronautical Science,
2:Osaka University,
3:Riken,
4:Massachusetts Institute of Technology,
5:Columbia University,
6:Goddard Space Flight Center
dotani@astro.isas.jaxa.jp
We report here the recent developments in the SIS calibration and the analysis software. Three topics are addressed: a new method of DFE correction, low energy calibration, and the non-uniform CTI. Some of the new calibration results have been incorporated in the FTOOLS version 3.5.
1 New method of DFE correction
It is crucial in spectral analysis to use the correct gain (i.e., slope and offset of the energy scale) of a detector. However, the energy scale offset (and maybe slope) of the SIS is not simple, and may depend on observation mode and time. We have developed new DFE (dark frame error) correction software to minimize the systematic effects on the energy scale offset. As explained below, the new software affects not only the energy scale offset but also the detection efficiency. We first explain the definition of zero of the energy scale, and then the algorithm of the new DFE correction software. The impact on the spectral analysis is explained afterward. This new DFE correction software has been implemented and is available from version 3.5 of FTOOLS.
1.1 Definition of zero
We use the pulse height distribution of pixels to define the zero energy scale. When neither an X-ray photon or charged particle hits the CCD and the radiation damage of the CCD is negligible, the pulse height distribution of pixels has an approximately gaussian profile. This is because the dark current is negligible and the pulse height distribution is determined by the readout noise. In this case, the definition of the zero energy scale is the center of the gaussian.
The zero energy scale is calculated on board for each 16 x 16 pixel region. To avoid contamination from the X-ray and particle events, a truncated mean is used to estimate the center of the pulse height distribution. The running average of the truncated mean of several consecutive exposures is calculated to smooth the statistical fluctuations. This running average is called a dark frame, and is used on board to correct the pulse height of each pixel. Because it takes at least several tens of seconds to update the dark frame, the dark frame calculated on board may not catch up with any rapid changes of the light leak, such as due to the day/night transition. The difference between the on-board dark frame and the true zero is called dark frame error (DFE), which may be corrected in the ground processing. Explanation of DFE and it's correction scheme is found in [1].
When the radiation damage becomes significant, the pulse height distribution is no longer a gaussian, but rather has a prominent tail toward higher energies. This is explained by the large increase of dark current in some pixels due to the radiation damage. This asymmetrical pulse height distribution is called RDD (residual dark distribution), because the asymmetry remains even after the DFE correction. Definition of the zero energy scale is somewhat arbitrary for the asymmetrical distribution of RDD. However, RDD has various effects on the SIS performance, and the effect is highly dependent on the definition of zero that is used. Thus we should define a zero energy scale that minimizes the impact on the SIS performance. Even when we use such a definition of zero, some effects still remain on the SIS performance that must be included in the SIS response matrices.
Before presenting the definition of zero, we introduce several terms related to the RDD.
Figure 1: Schematic pulse height distribution of CCD pixels under the effect of RDD. The pulse heights corresponding to the peak, the truncated mean and the global mean of the distribution are indicated.
Global mean
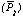 This is a mean value of the pulse height calculated from the pulse height data
of all pixels.
This is a mean value of the pulse height calculated from the pulse height data
of all pixels.
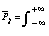 q x RDD
q x RDD
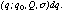 (1)
(1)
where RDD
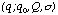 [1]
is a pulse height distribution under the RDD effect normalized to unity. This
is a new zero level definition adopted in FTOOLS version 3.5 and can be
calculated with the new "faintdfe" (zerodef = 1).
[1]
is a pulse height distribution under the RDD effect normalized to unity. This
is a new zero level definition adopted in FTOOLS version 3.5 and can be
calculated with the new "faintdfe" (zerodef = 1).
Truncated mean
 This is a self-consistent solution of the following formula:
This is a self-consistent solution of the following formula:
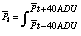 q x RDD
q x RDD
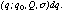 (2)
(2)
This corresponds to the on board zero when there is no light leak. The new "faintdfe" uses this definition when zerodef = 2.
Peak This is the pulse height at which the distribution peaks. Old "faintdfe" effectively searches for the peak of the distribution. The new "faintdfe" uses this definition when zerodef = 0.
These means/peak are schematically explained in figure 1. The old version of "faintdfe" effectively looks for the peak of distribution, and adjust the energy scale such that the peak becomes zero. If we use this zero, more and more pixels tend to have higher pulse height with the increase of the radiation damage. This has basically two effects on the SIS performance [2]:
1. Increase the energy scale offset and shift the line energy to
systematically higher values.
2. Pushes X-ray events to higher grades and, if we use grade 0, 2, 3, and 4,
reduces the quantum detection
efficiency.
Such systematic effects will be reduced by using the "global mean" as the zero energy scale.
1.2 Energy scale offset
We show in figure 2 the history of the Ni line energy in the SIS internal background. Two plots are shown in the figure; one uses the peak as the zero in the DFE correction, and the other uses the global mean as zero. Because the RDD effect is most significant in 4 CCD mode [2], the difference of the two plots is most significant in 4 CCD mode data. If we adopt the peak as zero of the energy scale, the Ni line energy gradually increases with time after the CTI correction. This is an artifact due to the RDD effect. If we adopt the global mean as zero, this effect is hardly visible. The systematic effect in the energy scale offset becomes very small with the new definition of zero.
Figure 2: Long-term history of the Ni line energy in the internal background of SIS. The first panel is SIS-0 and the second panel SIS-1. Filled symbols represent data processed using the global mean as zero, and open symbols those processed with the peak as zero, in the course of DFE correction.
1.3 Detection efficiency
We show in figure 3 simulated energy spectra of 3C273 assumed to be observed in 4 CCD mode. The data are processed using the new "faintdfe" in three different ways: one uses the peak as zero, another uses the truncated mean as zero, and the other the uses global mean as zero. The difference in the detection efficiency is apparent. The decrease of the detection efficiency is largest when we use the peak as zero, and is smallest when we use the global mean as zero.
Figure 3: Simulated spectra of 3C273 in 4 CCD mode at the epoch of Nov. 30, 1997. The data are processed by the new "faintdfe" with three different options. One uses the global mean as zero (solid line), another uses the truncated mean (dotted), and the third the peak (dashed). A reduction in the detection efficiency is minimized when the global mean is used as the zero level. Bright mode data uses the truncated mean method.
If we adopt the peak as the zero energy scale, many pixels tend to have high pulse heights due to the high energy tail of the RDD. Some pixels have even higher pulse height than the split threshold (40 ADU). With such pixels, a single event may be falsely classified as a split event (grade 2, 3, 4), and a split event as a higher grade event (grade 5, 6, 7). Thus, an X-ray event tends to be classified as a non X-ray event and this reduces the quantum detection efficiency. As seen from the figure, this reduction of the detection efficiency is almost energy independent.
1.4 Recommended choice of zero
In FTOOLS version 3.5 (or later), "faintdfe" has 3 choices of zero energy scale, i.e., zerodef = 0 (peak), zerodef = 1 (global mean) and zerodef = 2 (truncated mean). Depending on the data mode you are working on, you should choose the appropriate definition of zero.
If only the faint mode data are being processed, zerodef = 1 (global mean) should be used. This will minimize the RDD effect. However, because the RDD effect is not significant in 1-CCD mode data at present, different choice of zero will not produce a major difference in 1-CCD mode data.
When mixing the Faint mode and Bright mode data, there are several choices.
(i) If most of the data are in Faint mode, you may just discard the Bright mode data.
(ii) If the Bright mode data are taken during the satellite night, you can use zerodef = 2 to correct the DFE of the Faint mode data and add in the Bright mode data, because DFE during the satellite night is stable and predictable. "Faintdfe" with zerodef = 2 will correct DFE of the Faint mode data and adjust the zero energy scale to that of the Bright mode data, so that the Faint and the Bright mode data can be added consistently. Of course, you need to use response matrices of the Bright mode data for such data. When an observing plan includes the use of Bright mode, the mission operation team at ISAS usually tries to allocate Bright mode to the satellite night time.
(iii) If most of the Bright mode data are taken during the satellite day time and you want to combine Bright mode and Faint mode data, there is no simple choice. Try several different methods, i.e., zerodef = 1, zerodef = 2, or no DFE correction, to estimate the energy scale uncertainties.
(iv) The option of zerodef = 0 is not recommended, it is supplied for backward compatibility.
2 Low energy cal
In this section, we outline the calibration made to determine the detection efficiency of SIS (plus XRT) at low energies. To determine the low energy efficiency, we consider (1) the thermal shield of XRT, (2) the effective area of XRT, (3) the optical blocking filter of SIS, and (4) the dead layer of CCD. In addition, radiation damage of the CCD changes the apparent detection efficiency as explained in the previous section. We cannot use the flight data to independently calibrate the 4 items listed. For example, both the thermal shield and the optical blocking filter have an aluminum coating, and their thickness cannot be determined separately. Thus, we calibrate just the total efficiency, not the efficiency of each component.
2.1 Calibration with 3C273
We assumed that the XRT response (including the effective area) and the GIS response are well calibrated using the Crab and other data. Because the Crab is too bright for SIS to get useful data, we used 3C273 to calibrate the SIS. The >1 keV energy spectrum of 3C273 is approximately a power law, but the slope is time variable. Thus we calibrated SIS to give the same energy index as that of GIS using the data from exactly the same time interval for SIS and GIS. Because the observation of 3C273 was done in December 1993, the effect of the radiation damage should be small, but cannot be neglected. Finally, the energy spectrum of 3C273 may not be a power law; we will discuss this point later.
The method of SIS calibration with 3C273 data is as follows. We have 4 pointings in the 3C273 observations. The source was put on each chip and the data were obtained in 1-CCD Faint mode with that chip.
1. Calculate the GIS spectrum of 3C273 for each set of data. The energy spectrum is fitted with a power law above ~3 keV and the power law index is determined for each pointing.
2. Calculate the SIS energy spectra of 3C273 using the latest calibration data. DFE and CTI corrections are carefully made.
3. Using the SIS energy spectrum above ~3 keV to calibrate the depletion layer thickness of each chip by adjusting it
to give the same energy index as the GIS spectrum.
4. The combined low energy absorption by nitrogen, oxygen, silicon and aluminum are adjusted such that a simple
power law modified by the Galactic absorption fits the data. Absorption by hydrogen and carbon is effectively
adjusted by nitrogen.
Figure 4: Flow of SIS calibration method with the 3C273 data. The above method is illustrated in figure 4.
The depletion layer thickness determined with the 3C273 data is between 26--33 um and is consistent with the ground calibration (3). We show in figure 5 an example of detection efficiency of SIS calibrated using 3C273 data. Two efficiency curves are shown in the figure. One is based on the ground calibration data and telescope ray tracing. The other uses the flight calibration with the 3C273 data. Although there is a difference in the detection efficiency between the two sets of calibrations, it is small, at up to ~10% level. The low energy efficiency we obtained is on average slightly lower than that of the ground calibration. Possible origins of this difference are: (1) the uncertainty of the XRT, GIS and SIS responses; (2) the radiation damage of SIS; (3) an accumulation of hydrocarbons on XRT or the optical blocking filter of SIS; (4) the calibration error of the thickness of the thermal shield, the optical blocking filter or the dead layer of the CCD. It is noteworthy that, if a soft excess is present in 3C273, the quantum detection efficiency at low energies should be reduced further. Further investigations are underway to understand these discrepancies.
2.2 Features around 0.5 keV
A power law (modified by the Galactic absorption) model generally fits the observed energy spectra of 3C273 well, but some residual structures remain around 0.5 keV. There is an oxygen edge structure at 0.532 keV in the SIS detection efficiency, and the residual structure of 3C273 is most significant around this edge structure. Thus the residual is suspected to be an artifact due to a slight difference between the observed and model edge energy.
It is essential to use the correct energy scale (offset and slope) to reproduce the edge structure accurately. However, the apparent edge energy of oxygen in the observed spectra may vary from observation to observation mainly for two reasons: one is the error of DFE correction and the other is the uncertainty of CTI. The optical light leak changes with time, sometimes as rapidly as 102 sec.
Figure 5: The quantum detection efficiency of SIS (sensor 0, chip 1) based on the ground calibration (dashed line) and the flight calibration with 3C273 (solid line).
The DFE correction tries to remove such time-dependent changes of energy scale offset due to the light leak, but its accuracy is limited by the available number of events. CTI may also change from observation to observation depending on the X-ray flux of the source. Moreover, the optical light leak, which depends on the satellite attitude, tends to reduce the CTI , which changes the energy scale slope (and possibly the offset). Thus the apparent oxygen edge energy in the spectrum varies from observation to observation. This variation, which may be as small as 10 eV, has small effects at energies where the detection efficiency does not have sharp structures, but produces artificial structures at energies where the efficiency changes discontinuously, such as the oxygen edge and the Si edge. Because it is difficult to correct for the apparent variation of the edge energy in the observed spectra with enough accuracy, artificial structure around 0.5 keV is difficult to remove at present.
We have analyzed the structure around 0.5 keV for various sources. It is found that the structure becomes prominent below ~0.6 keV and the amplitude of structure is typically ~10% (see also the next subsection). Because the structure arises from the slight deviation of the energy scale offset, the structure changes greatly when the offset is adjusted using the gain command of XSPEC. However, the adjustment should be kept to be within ~10 eV. The structure around 0.5 keV which changes greatly with an adjustment of the offset is most probably an artifact.
2.3 Other calibration targets
It is suspected that the energy spectrum of 3C273 is not intrinsically a power law but has a soft excess. The soft excess is probably not detected by GIS. If the soft excess made a significant contribution in the ASCA SIS energy band when the calibration observations of 3C273 were made, the current low energy SIS calibration may have systematic errors. Thus, independent calibrations of the low energy response should be useful. For this purpose, we analyzed the data on 3C58 and the Coma cluster of galaxies. The analysis was done using the FTOOLS version 3.4 or earlier.
3C58 is a Crab-like SNR and the energy spectrum is believed to obey a power law. It has a relatively small absorption column (for SNR) and, of course, has no time variability. 3C58 was so far observed with various satellites including Einstein, EXOSAT, and Ginga. Thus the photon index is relatively well constrained (above ~2 keV). The ROSAT PSPC data were found to be not useful because of a gain problem.
Figure 6: The best fit photon index
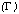 and the equivalent hydrogen column density (NH) of 3C58 from various sets of
data. Contours are 90% confidence region obtained with the combined data of
Einstein SSS, Einstein MPC and Exosat. Ginga LAC gives only the upper limit of
NH. Error bars of the best fitting values of SIS and GIS are 90% confidence
limit for a single parameter. The neutral hydrogen column density obtained
from 21cm measurements is 0.65 x 1022 cm-2.
and the equivalent hydrogen column density (NH) of 3C58 from various sets of
data. Contours are 90% confidence region obtained with the combined data of
Einstein SSS, Einstein MPC and Exosat. Ginga LAC gives only the upper limit of
NH. Error bars of the best fitting values of SIS and GIS are 90% confidence
limit for a single parameter. The neutral hydrogen column density obtained
from 21cm measurements is 0.65 x 1022 cm-2.
ASCA observations of 3C58 were made in September 1995. Data were obtained for 3 chips (chips 0, 1, 2 for SIS-0 and chips 0, 2, 3 for SIS-1) and the 4th pointing was used to obtain background data. The energy spectra were calculated for each chip, and a power law model modified by an absorption was fitted. The results are shown in figure 6 together with those of the previous results. The finite source size was taken into account in making the ARF file, but has little effects on the photon index and NH.
The hydrogen column density values obtained from the ASCA data are in general slightly larger than the Einstein + EXOSAT and the Ginga values. GIS and SIS-0 give almost the same column density, but SIS-1 prefers a slightly higher value. Several reasons are conceivable for the slightly higher NH obtained with ASCA: (1) the energy spectrum of 3C58 may deviate from a power law below ~2 keV, (2) the abundance of the absorbing material in the line of sight to 3C58 may not be solar, (3) dust scattering may modify the apparent shape of the spectrum, or (4) the contamination on XRT may have modified the response. As for the slight difference of the parameters between SIS-0 and SIS-1, there are also several possible origins: (1) a calibration error of the thickness of the absorption layer (the thermal shield, the optical blocking filter, and the dead layer of CCD), (2) a calibration error in the depletion layer of CCD, (3) a difference in the radiation damage, (4) a difference in the optical light leak, or (5) a calibration error of the position of the optical axis. Our current understanding of the detector characteristics is not advanced enough to distinguish the various possibilities. The SIS calibration currently in progress is expected to clarify the origin of these differences.
The residual structure around 0.5 keV was investigated with the data of the Coma cluster of galaxies (A1656). Coma cluster has a relatively high temperature of ~10 keV and a low Galactic absorption (0.9 x 1020 cm-2). Thus it is expected to have a relatively simple spectrum of lower energies. The data were obtained in June 1993. The model energy spectrum used to fit the data is a Raymond-Smith model modified by the Galactic absorption. The Galactic absorption (0.9 x 1020 cm-2) and the red shift (z = 0.0235) were fixed in the course of the model fitting. We found that the residual structure around 0.5 keV show large variations from chip to chip and there was no clear systematic trend. The amplitude of the residual structure was at most ~10% level. If we let the absorption be free in the fitting, the best fit value increased for some chips by about 2 x 1020 cm-2. Thus, we consider that current estimate of hydrogen equivalent column density has a systematic error of about 2 x 1020 cm-2.
2.4 Future calibration
The calibration of the SIS with 3C273, XRT and GIS responses have been updated. Furthermore, introduction of a so-called "filter file" is planned to reduce the systematic structures seen in the residuals of the GIS Crab spectrum. As explained in figure 4, SIS (+XRT) calibration was done to give consistent results with GIS (+XRT). Thus, once the XRT or GIS responses are revised, the SIS calibration should be re-done with the new responses. Re-calibration of SIS with the latest XRT and GIS responses (and "arf filter") is now under way.
The previous calibration of the SIS was based on the assumption that the energy spectrum of 3C273 can be well approximated by a power law modified by the Galactic absorption. However, this assumption may not be correct. There may be soft excess over the power law in the soft energy band. The soft excess seems to be time variable, and hence it may not be easy to incorporate the soft excess into the calibration. Possible systematic errors in the response due to the soft excess will be evaluated in the near future.
3 Non-uniform Charge Transfer Inefficiency (CTI)
The CTI has gradually been increasing since the launch of ASCA. It had been assumed to be uniform over a CCD chip, but a detailed analysis of recent data showed that the CTI is now significantly non-uniform. In this section, we explain the analysis we have done on the uniformity of CTI and its impact on the SIS response. Energy resolution degradation due to the non-uniform CTI is incorporated in the SIS response from FTOOLS version 3.5.
3.1 CTI measurements with Cas A data in 1995
We observed Cas A at 4 different pointing positions on the standard chips in August 1995. Because this is more than the minimum number of 3 pointings necessary to calculate parallel and serial CTI, we could check the uniformity of CTI. The number of pointings on standard chips were 2 in 1993 and 3 in 1994. Thus, such an analysis became possible for the first time in 1995.
Figure 7: The pointing positions on the standard chips in 1995 Cas observations. Using these 4 pointings of data, we can determine two parallel CTIs, Cp1 and Cp2, independently.
Using these data we can determine parallel CTI at two different regions. One is between o and h and the other is between v and x. We first calculated the difference of apparent line energies between the pointing positions using Si, S, Fe lines. We then calculated the CTI assuming if is constant against photon energy, i.e. charge lost by CTI is proportional to the original charge packet size. For example, Cp1 is calculated from the line energy differences between v and x, and Cp2 from the line energy differences between o and h. The results are listed in table 1. Expected CTIs, which are extrapolated from the CTI determined by Cas A data in 1994, are also listed in the table.
_______________________________________________________________________________
Parallel CTI (x10^-5/tr) Serial CTI (x10^-5/tr) Chip Cp1 Cp2 Extrapolation^a Cs Extrapolation^a _______________________________________________________________________________________________________________________________________________________________S0C1 6.2+/-0.5 2.2+/-0.4 4.0 11.4+/-0.5 5.3
S1C3 6.5+/-0.5 3.6+/-0.4 4.1 4.9+/-0.1 -0.4
Errors are in 90% confidence limit.
Extrapolated CTI from the value in July 1994.
As seen from table 1, the difference of parallel CTIs with position, Cp1 and Cp2, are large. The serial CTIs are also very different from the extrapolated values based on 1994 measurements. This is because the serial CTI in 1994 measurement was determined under the assumption of uniform parallel and serial transfer (ST) CTI (CTI associated with ST clock i.e., charge transfer from the imaging to frame store area), which is not the case. Even for the serial CTI determined from 1995 observations, the uniformity of the ST CTI is still assumed. If the ST CTI is not uniform over the chip, which is very plausible, serial CTI may be different from the value listed in the table. Because the number of transfers associated with the ST CTI is constant (422) for all the pixels in a chip, there is no way of directly measuring the ST CTI. According to the investigation above, it is suspected that non-uniformity of CTI is very large and may be comparable to the mean CTI.
3.2 Column to column variations of parallel CTI
The Cas A observation at the position of the standard chips has a relatively long exposure to obtain enough statistics for the iron line. This means that more than enough photons are available for the Si line. We can accumulate energy spectra with good statistics if we select events from a single column which lies under the brightest part of Cas A. Thus we can study column to column variations of the energy spectra. We calculated the energy spectra with grade 0 events of both the Bright mode data and the DFE-corrected Faint data. The Bright mode data were obtained during satellite night time, and hence the DFE stable. We show in Figure 8 the Si line energies calculated from the spectra constructed from single column data. The H-addresses (RAWX) of the columns are 344--353 for S0C1 and 380--389 for S1C3. Thus the data cover 10 consecutive columns, which correspond to 1/4 arcmin. This is much smaller than the HPD of XRT and the change of spectral parameters should have instrumental origin (not intrinsic to the source).
Figure 8: The Si line energies obtained from the single column energy spectra. The variations of the line center energies are due to the column to column variations of parallel CTI.
The standard deviations of the line center energies shown in Figure 8 are 22 eV for S0C1 and 48 eV for S1C3. Because the line center shift due to the parallel CTI is roughly 20 eV, this means that the relative variations of the parallel CTI from column to column amount to 100%.
3.3 History of the Cas A line profile
The current CTI correction method assumes that CTI is uniform over a chip. The non-uniformity of CTI means that the current CTI correction method cannot restore the original energy resolution. This effect may be observed in the Cas A spectra. The Cas A data were taken in various modes with various pointing positions, but 1-CCD faint mode data were taken every year from the standard chips at exactly the same pointing position as a reference. We show in Figure 9 the energy spectra calculated from these reference data, which were obtained in August 1993, July 1994 and August 1995. The standard data selection was applied and the data were corrected for DFE, echo and CTI. The CTI values used are those determined from Cas A data in 1994 (2). Note that the RDD effect is negligible for 1 CCD data.
Figure 9: The Cas A spectra in: August 1993, July 1994 and August 1995 showing the degradation in energy resolution. The spectra were calculated from the data in 1-CCD Faint mode and were corrected for DFE and CTI.
As seen from figure 9, the degradation of the energy resolution is clear. This is due to the non-uniformity of the CTI.
3.4 Degradation of energy resolution
We calculated the widths of Si, S and Fe lines of Cas A as a function of observation time to evaluate the energy resolution degradation. The data used here are basically the same as those shown in figure 9. All these data were taken at the same pointing position of the standard chips, and were corrected for DFE and echo. The lines are intrinsically broad and hence line width has little intrinsic meaning. Measured line widths of Si, S and Fe are listed in table 2.
Sensor Element CTI corr. 1993 August 1994 July 1995 August _______________________________________________________________________________ SIS-0 Si yes 20.6+/-1.6 31.4+/-1.2 39.9+/-1.2 no 20.3+/-1.6 32.0+/-1.4 40.2+/-1.4 S yes 33.3+/-2.5 42.1+/-1.9 52.4+/-2.2 no 33.2+/-3.0 42.7+/-1.9 50.2+/-2.2 Fe yes 99.7+/-10.3 114.5+/-8.7 125.6+/-9.1 no 99.1+/-10.3 115.0+/-8.8 116.4+/-8.8 SIS-1 Si yes 21.8+/-1.0 33.4+/-1.2 43.5+/-1.3 no 22.2+/-1.2 36.0+/-1.3 44.9+/-1.5 S yes 32.5+/-1.5 44.0+/-2.2 53.8+/-2.6 no 32.4+/-1.7 44.8+/-2.2 52.8+/-2.3 Fe yes 87.4+/-7.7 107.2+/-9.0 125.4+/-10.7 no 87.5+/-7.8 104.2+/-9.1 118.2+/-10.31. Line widths listed are of gaussian model function in unit of eV and their errors are in 90% confidence limit.
2. Approximate line center energies are 1.85 keV (Si), 2.44 keV (S) and 6.58 keV (Fe).
We show in table 2 the line widths obtained before and after CTI correction. As seen from the table, CTI correction does not improve the energy resolution. This confirms that non-uniformity of CTI is very large and the small scale CTI variations are comparable to the CTI itself.
3.5 Empirical model
The energy resolution degradation due to the non-uniform CTI can be modeled as a change in the Fano factor with time. It is known that the statistical fluctuation of the number of electrons produced by an X-ray photon is smaller than that expected from the Poisson fluctuations. The Fano factor defines the size of fluctuation in comparison with the Poisson fluctuation. We assume that the Fano factor (f) changes linearly with time:
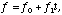 (3)
(3)
where
 is the Fano factor at launch time,
is the Fano factor at launch time,
 Fano factor variation coefficient (s^-1), t
time after the launch (sec). With this assumption, the apparent line width in
Fano factor variation coefficient (s^-1), t
time after the launch (sec). With this assumption, the apparent line width in
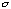 in eV can be represented as follows:
in eV can be represented as follows:
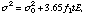 (4)
(4)
where
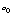 is the intrinsic line width (eV), E line energy (eV). It has been found that
this model function can reproduce the observed history of the Si, S, Fe line
widths quite well. The best fit coefficients we have obtained are
is the intrinsic line width (eV), E line energy (eV). It has been found that
this model function can reproduce the observed history of the Si, S, Fe line
widths quite well. The best fit coefficients we have obtained are
 sec-1 for SIS-0 and
sec-1 for SIS-0 and
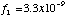 sec-1 for SIS-1. The best fit model functions are shown in Figure
10 with the observed line widths.
sec-1 for SIS-1. The best fit model functions are shown in Figure
10 with the observed line widths.
Figure 10: The time variations of the apparent line widths of Cas A and the best fit model function. The circles represent CTI correction data and the triangles represent data not corrected for CTI. The model function is fitted to the CTI-corrected data. The ASCA time at the launch is 0.432x10^7 sec.
The non-uniformity of the CTI is very large even on a microscopic scale in a chip, and hence it is suspected that the CTI fluctuates even from pixel to pixel. This means that, if we want to correct for CTI, we need to define the CTI for each pixel. This is equivalent to defining the gain for each pixel and hence practically impossible for SIS. Therefore, the only method we can apply is to include the energy resolution degradation due to the non-uniform CTI in the response matrices of SIS. This is done from the FTOOLS version 3.5 with the above model of the Fano factor.
References
[1] Otani C. et al., 1994 ASCA news No. 2, 25
[2] Dotani, T. et al., 1995 ASCA news No. 3, 25
[3] Gendreau, K. G. 1995 Phd thesis (MIT)
 Proceed to the next article
Proceed to the next article
 Return to the previous article
Return to the previous article


 Select another article
Select another article