Next: 8. Resolve Observations of Up: xrism pog Previous: 6. Xtend/SXI Contents
In this chapter, we present the characteristics of XRISM instruments that are relevant to the observations of extended sources. In particular, we discuss the possibilities and limitations of spatially-resolved spectral analysis given the imaging performance of XMA and the smaller FOV of Resolve. Careful simulations are often necessary to assess, at a reasonable degree of confidence, whether a particular spatial-spectral analysis objective is achievable.
The non-dispersive high-resolution spectroscopy offered by the Resolve instrument onboard XRISM allows one to observe extended sources (e.g., clusters of galaxies, supernova remnants) with an unprecedented spectral resolving power (Chapter 5). Similarly, theses sources can also be imaged and investigated spectrally (though at much lower spectral resolution) using Xtend (Chapter 6). However, the limited spatial resolution permitted by the observatory (as well as the limited number of pixels on the Resolve detector) requires extra caution from observers of these systems.
The two main limiting properties of Resolve are:
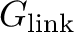 , i.e. substantially smaller than the PSF (
, i.e. substantially smaller than the PSF (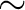 1.3 arcmin HPD);
1.3 arcmin HPD);
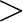 (i.e. of size comparable to the PSF).
(i.e. of size comparable to the PSF).
The Xtend instrument has a larger field of view and, therefore, is not affected by the latter limitation. The PSF, however, is a characteristic of the XMA (Chapter 4) and thus affects Resolve and Xtend in a similar manner..
As a consequence, in both instruments photons from specific regions of the sky are expected to spread over the detector and “contaminate" (more specifically, mix with photons from) other regions. Given that this process occurs at all energies, this mixing will affect the source not only spatially but also spectrally. In the following, we refer to this process as “spatial-spectral mixing" (SSM).
Concretely, and depending on the extent, properties and environment of the source, Resolve can be affected by two types of SSM:
|
|

|
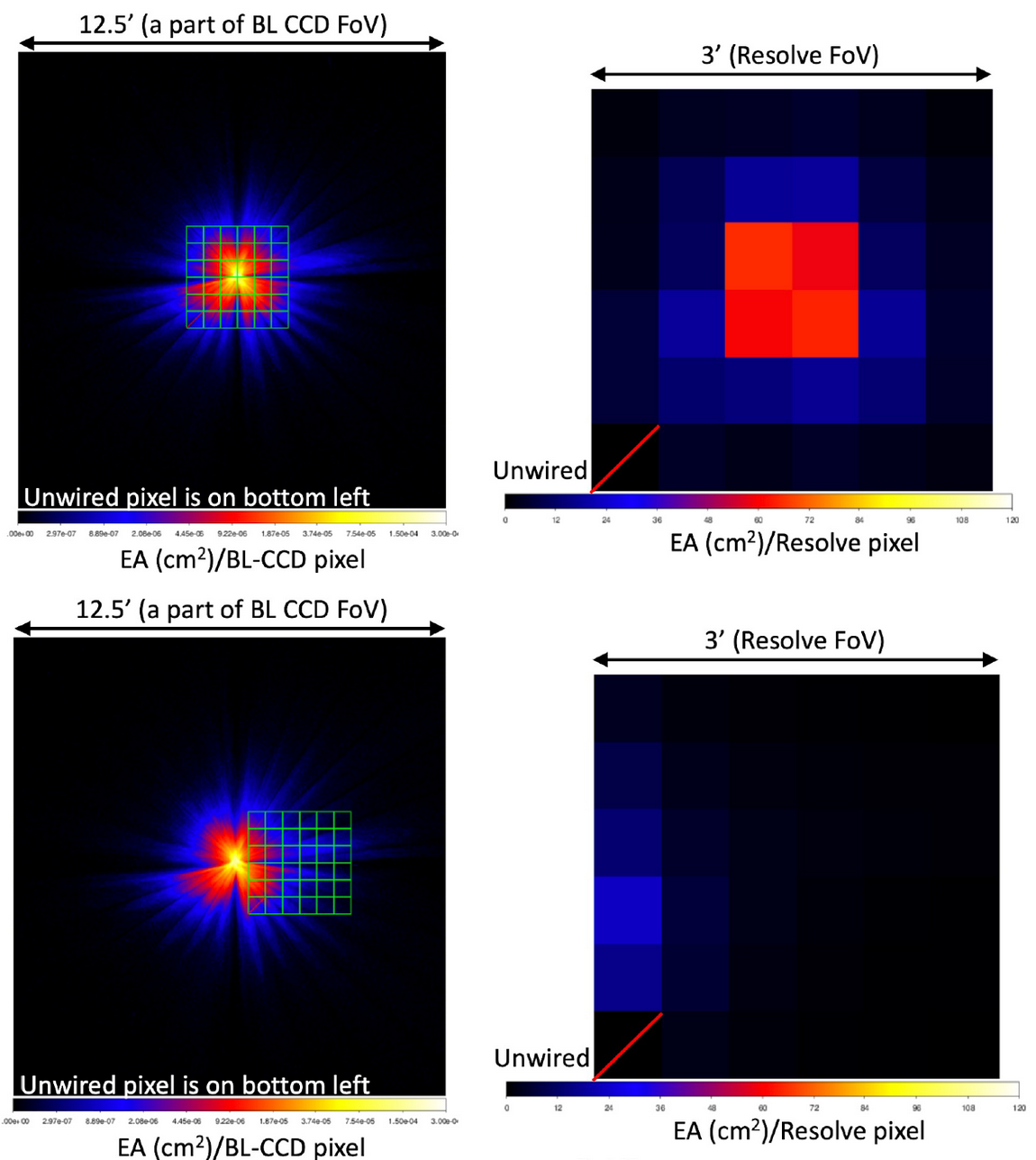
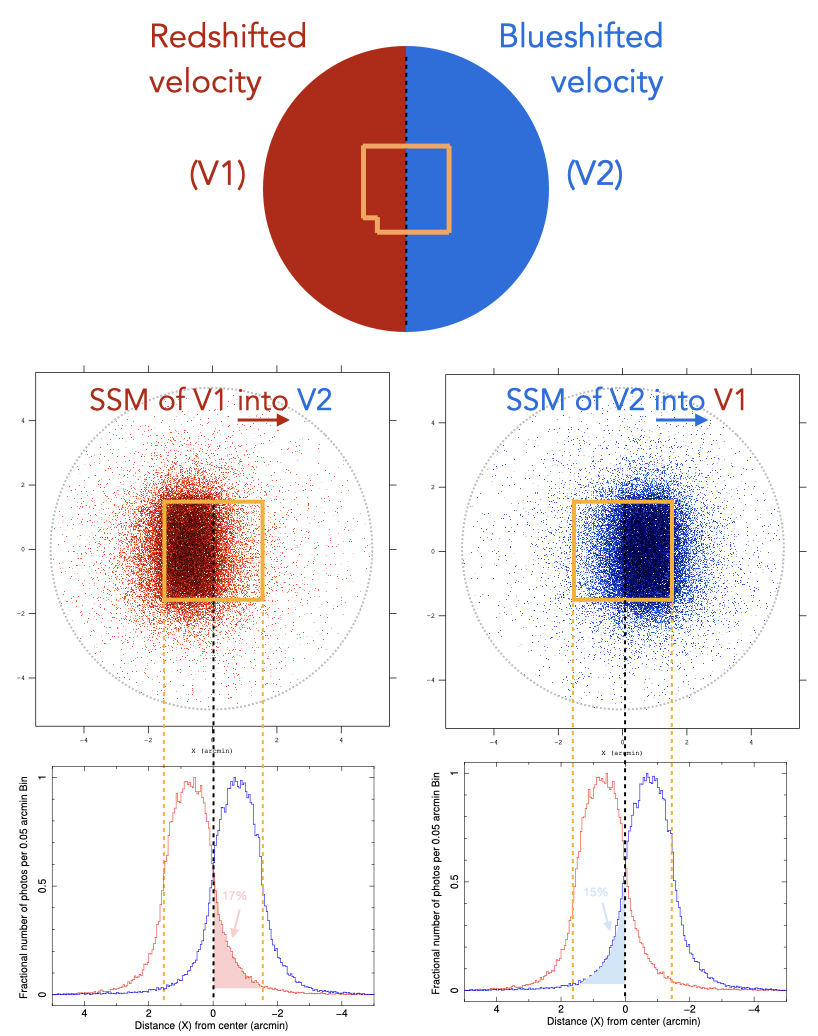
The external and internal SSM are illustrated in Figure 7.1 for the simple case of photons from a single point-like source spreading over the detector. As seen on the figure, due to mirror support structures, imperfect alignments of telescope components, mirror foil figure errors, and non-ideal foil surfaces, the PSF has a complex shape and is not azimuthally symmetric. Particularly in the case of a complex extended structure (e.g., with resolved point sources, clumps and/or hot spots), the PSF effects cannot be seen as a simple Gaussian-like smoothing of an ideal image and should be thus addressed carefully and accurately. The next two figures (Figs. 7.2 and 7.3) focus on a concrete (though very simplistic) case of a circular extended source, half of which is redshifted (V1 = +235 km 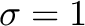 ) while the other half is blueshifted (V2 =
) while the other half is blueshifted (V2 = 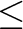 235 km
235 km 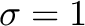 ). At first approximation, this is close to what is expected for galaxy clusters with rotating bulk motions of their hot haloes. The spectral effects of the PSF mixing of that specific source are shown in Figure 7.3. Quite interestingly, a mixing of the two components with equal fluxes (e.g., if one looks at central region covering the two components simultaneously) produces a double-peaked line profile, much easier to identify and interpret than the asymmetrical profile seen when one component dominates over the other (e.g., if one looks at a region with one component – though inevitably affected by SSM still).
). At first approximation, this is close to what is expected for galaxy clusters with rotating bulk motions of their hot haloes. The spectral effects of the PSF mixing of that specific source are shown in Figure 7.3. Quite interestingly, a mixing of the two components with equal fluxes (e.g., if one looks at central region covering the two components simultaneously) produces a double-peaked line profile, much easier to identify and interpret than the asymmetrical profile seen when one component dominates over the other (e.g., if one looks at a region with one component – though inevitably affected by SSM still).
Generally speaking, the SSM issues described above are somewhat less impactful for Xtend as its PSF (although of similar size as in Resolve) is much smaller than its field of view. Except in specific cases, a moderately extended source placed on axis of the (large) Xtend field of view will thus make the external SSM less important in comparison, and it will be easier to quantify the internal effects of the PSF mixing within the source. Moreover, the moderate spectral resolution of Xtend means that there will inevitably be less subtle spectral features to be affected by SSM. This, however, does not mean that SSM effects can be neglected when analyzing extended sources with Xtend. In fact, variations from e.g., bright emission lines (and/or the continuum) are still important to take into account even at CCD resolution.
The “advantage” of the SSM from Xtend is that the issue is not new. In fact, such effects have affected extended sources in very similar ways in previous missions such as ASCA or Suzaku. For this problem, we thus refer the proposer to the literature which abound with many concrete cases (for the case of galaxy clusters, see e.g., Bulbul et al., 2016; Bautz et al., 2009; Markevitch et al. , 1996). In contrast, the above-mentioned characteristics of Resolve make (internal and external) SSM issues more complicated and relatively unexplored (see however the case of the Perseus cluster observed by Hitomi; e.g., Hitomi Collaboration , 2018). The rest of this chapter will therefore focus primarily on Resolve.
As mentioned earlier, the problem of SSM is not completely new, as it has already been encountered to some extent in other X-ray missions – in particular those with a large PSF, such as Suzaku and NuSTAR. The spectral analysis of X-ray extended sources in those cases is often performed as follows:
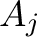 ) as well as an associated ARF (
) as well as an associated ARF (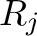 ) that best describes the source. In most cases, the same RMF (
) that best describes the source. In most cases, the same RMF (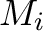 ) can be assumed for all regions as it weakly varies across the detector;
) can be assumed for all regions as it weakly varies across the detector;
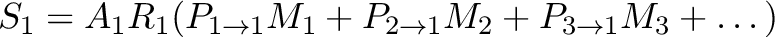 is associated with each spectrum
is associated with each spectrum 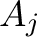 as follows:
as follows:
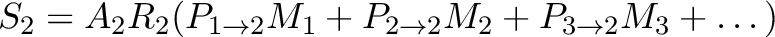 |
(7.1) |
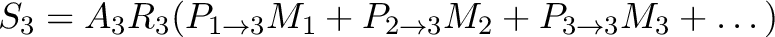 |
(7.2) |
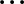 |
(7.3) |
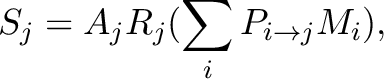 |
(7.4) |
Under a more generic form, one has:
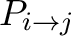 |
(7.5) |
where
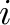 are coefficients corresponding to the relative contribution of the model
are coefficients corresponding to the relative contribution of the model 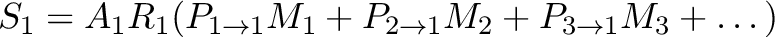 in the spectrum
in the spectrum 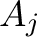 . In an ideal case with no contamination at all, the
. In an ideal case with no contamination at all, the
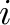 matrix is in fact diagonal. Even in more realistic cases, many
matrix is in fact diagonal. Even in more realistic cases, many
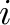 terms may be negligible (particularly if regions
terms may be negligible (particularly if regions 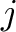 and
and 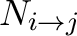 are more than a few arcmin away), however the SSM will inevitably make several other
are more than a few arcmin away), however the SSM will inevitably make several other
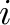 values positive.
values positive.
|
To estimate numerically each value from the
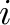 matrix, a tempting approach would be to associate them directly with the normalization parameter of each model
matrix, a tempting approach would be to associate them directly with the normalization parameter of each model 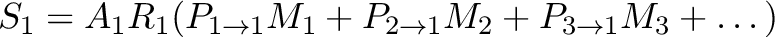 in simultaneous fits of all spectra
in simultaneous fits of all spectra 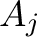 . Such normalization parameters (
. Such normalization parameters (
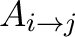 ) would then be left free in the fits. This method, however, is strongly discouraged for a number of reasons. First, thawing all these normalizations considerably increases the number of free parameters in the fits, with a high risk of reaching strong degeneracies between the latter and/or local minima in the fits. Also, the best-fit values of the free
) would then be left free in the fits. This method, however, is strongly discouraged for a number of reasons. First, thawing all these normalizations considerably increases the number of free parameters in the fits, with a high risk of reaching strong degeneracies between the latter and/or local minima in the fits. Also, the best-fit values of the free
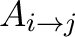 coefficients may not reflect the true mixing rate in the considered region (as such normalizations could be biased by other unaccounted uncertainties). In fact, free normalizations between the matrix elements uncouple the problem from the actual telescope and detector, making a “black box” of the whole SSM issue, and will thus likely give artificial results. Such approach should be thus avoided by all means, particularly in the case of Resolve observations.
coefficients may not reflect the true mixing rate in the considered region (as such normalizations could be biased by other unaccounted uncertainties). In fact, free normalizations between the matrix elements uncouple the problem from the actual telescope and detector, making a “black box” of the whole SSM issue, and will thus likely give artificial results. Such approach should be thus avoided by all means, particularly in the case of Resolve observations.
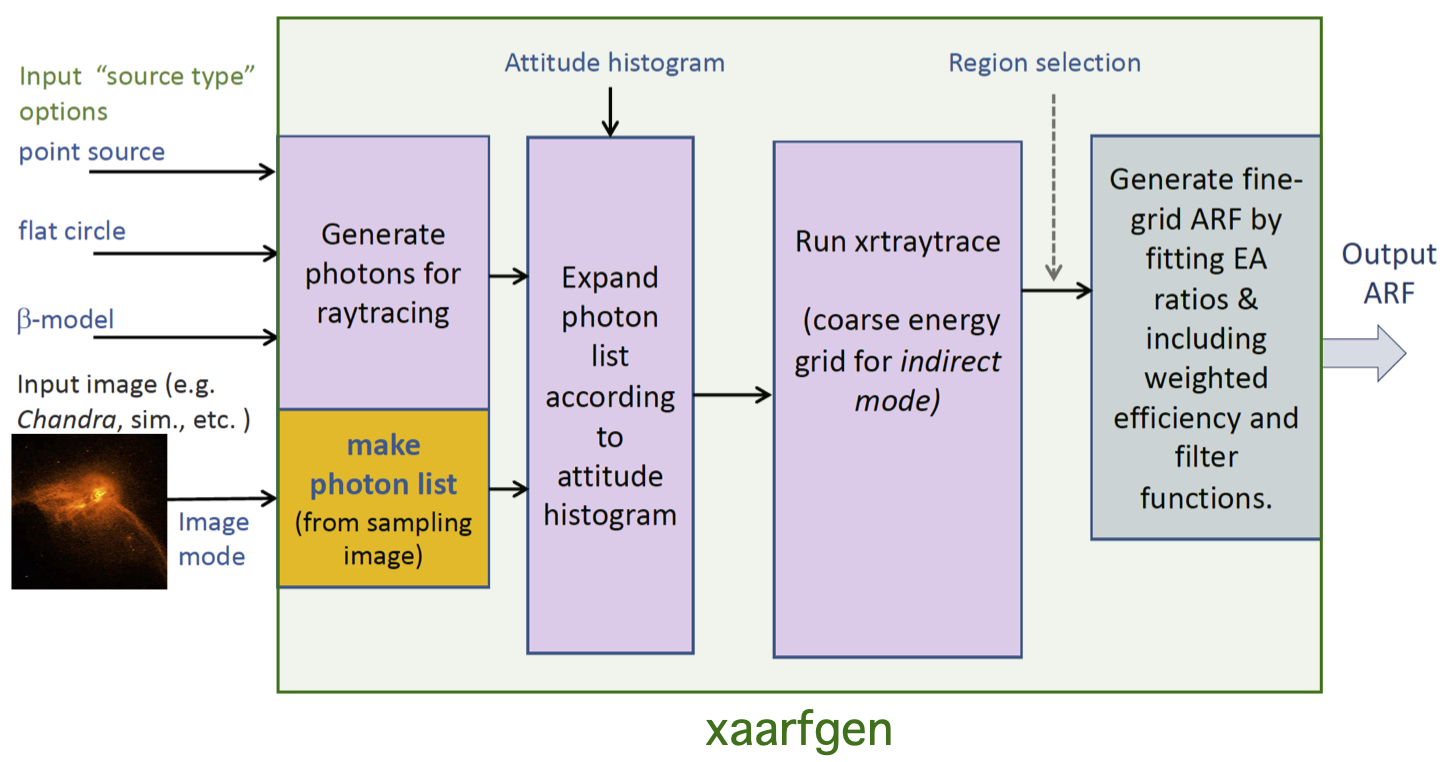
A much more accurate way to proceed is to determine these coefficients directly by calculating (i.e. via ray-tracing) the contribution of each component from region 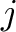 into a considered region
into a considered region 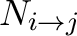 . This can be done from the XRISM data reduction software by the routine xaarfgen (Figure 7.4) which, via its ray-tracing subroutine xraytrace, generates an ARF that can be applied directly on a given model
. This can be done from the XRISM data reduction software by the routine xaarfgen (Figure 7.4) which, via its ray-tracing subroutine xraytrace, generates an ARF that can be applied directly on a given model 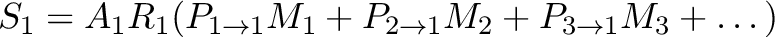 . The obtained effective area has been specifically scaled by the routine to account for the exact contribution from region
. The obtained effective area has been specifically scaled by the routine to account for the exact contribution from region 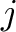 into region
into region 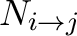 , meaning that the normalization parameter of each model
, meaning that the normalization parameter of each model 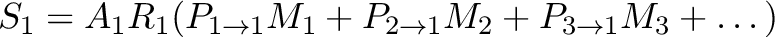 remains untouched (thus, it conserves its initial physical interpretation). The subroutine xraytrace is able generate such ARFs from a geometrically simple input model (e.g., point source,
remains untouched (thus, it conserves its initial physical interpretation). The subroutine xraytrace is able generate such ARFs from a geometrically simple input model (e.g., point source,  model) or even an input image; e.g,. taken from Chandra/ACIS, XMM-Newton/EPIC, or simply from a simulation7.1. Adopting this method, the
model) or even an input image; e.g,. taken from Chandra/ACIS, XMM-Newton/EPIC, or simply from a simulation7.1. Adopting this method, the
 values have their information directly encoded in a grid of ARFs generated specifically for this purpose (
values have their information directly encoded in a grid of ARFs generated specifically for this purpose (
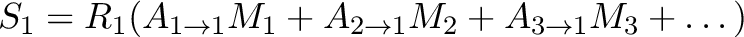 ), and the above system of equation becomes then:
), and the above system of equation becomes then:
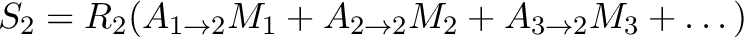 |
(7.6) |
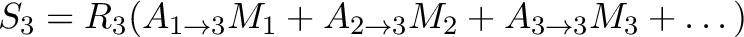 |
(7.7) |
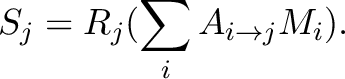 |
(7.8) |
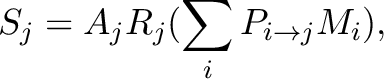 |
(7.9) |
 |
(7.10) |
In the case of Resolve, it becomes then tempting to follow the same method with, for bright and very extended objects, up to 35 regions (each corresponding to one active pixel on the detector). However, the wealth of spectral information delivered by XRISM associated with the complexity of the ray-tracing process used for the mission requires computing resources that may become considerably heavy. In fact, the computing time requested for ray-tracing in the “fast-mode” (i.e. with more limited off-axis accuracy) and extracting a single ARF can easily exceed the hour, making the above approach extremely time-consuming (i.e. on the order of days or even weeks for standard single machines).
Besides the use of distributed/pseudo parallel computing (if available at the user's host institute), a library of pre-computed PSFs (as a function of the energy, off-axis angle, azimuthal angle) will be made available for Resolve after the launch of the mission. The sum of contributions will then generate a series of fine-grid effective areas for the spectral regions considered. Another alternative to reduce computing times is to focus on a small energy range7.2 (if permitted by the science goal) and/or reduce the number of ray-tracing photons. Also, since the SSM is due to the telescope, the ray-tracing code xrtraytrace as part of the XRISM data analysis software can be used to make SSM estimates by running standalone for single energies. For proposals and/or actual analysis of real data, one can still use the above approximate methods to make an initial assessment of which cross-mixing elements are negligible (e.g,. two regions that are distant from each other). Doing so, the run time for creating the full ARFs is not wasted on ARFs that can be safely omitted.
As we have seen in the previous two sections, the analysis of extended sources with XRISM is possible, but challenging. To help proposers evaluate to what extent their science goal is feasible, we provide in this section a list of items and considerations that are important to keep in mind at all stages of the observation – from the proposal to the analysis.
We stress that this list is purely indicative, non-exhaustive, and does not constitute a formal checklist for the technical feasibility of any future proposal.