Next: 9. In Depth Discussions Up: xrism pog Previous: 7. Spatial-Spectral Mixing: Extended Contents
Bright sources uniquely enable precise measurements of variability and detection of very weak lines at high significance, but the high count rates associated with these sources pose several challenges: the count rate becomes dominated by low-resolution events, the onboard event processor becomes saturated and loses events, the energy resolution in some pixels degrades due to electrical cross-talk, and some pixels develop gain shifts as the detector structure heats up due to the energy flux (Mizumoto et al. , 2025b,a). The net impact is fewer clean, high-resolution events than expected. This chapter summarizes these challenges and offers suggestions for observing bright sources.
These effects become relevant above 100 counts s across the array and quite pronounced above 200 counts s
across the array and quite pronounced above 200 counts s . For a typical power law, this corresponds to a 0.3-10 keV flux
. For a typical power law, this corresponds to a 0.3-10 keV flux
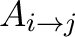 or
or 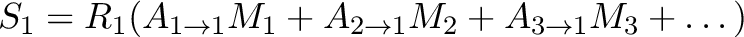 erg s
erg s cm
cm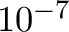 , equivalent to about 200 or 400 mCrab. Note that the Crab nebula's X-ray flux is defined as
, equivalent to about 200 or 400 mCrab. Note that the Crab nebula's X-ray flux is defined as 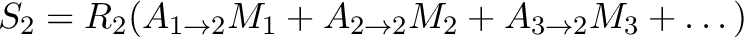 keV
keV
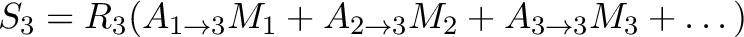 erg s
erg s cm
cm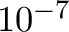 (Willingale et al., 2001). For most science cases, mitigation at the proposal stage only becomes necessary for 2-10 keV
(Willingale et al., 2001). For most science cases, mitigation at the proposal stage only becomes necessary for 2-10 keV
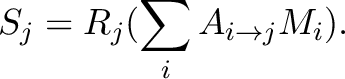 erg s
erg s cm
cm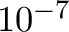 . Almost all persistent “bright” sources are well-known Galactic compact objects (see
. Almost all persistent “bright” sources are well-known Galactic compact objects (see
https://heasarc.gsfc.nasa.gov/docs/heasarc/headates/brightest.html). Since the Crab Nebula is the only current extended source with a count rate that falls in this regime, observing strategies assume point-like sources; for observing the Crab itself, please see (Mizumoto et al. , 2025b).
We note that bright sources to Resolve will be piled up in Xtend when using full-frame imaging mode, as a “bright” source to Xtend is about thirty times dimmer. Chapter 6 describes the impact of high count rates on event detection (pile-up and out-of-time events) and the observing modes available to mitigate issues. For almost any bright source, the optimal Xtend observing mode is a windowed burst mode.
As described in Section 5.3.3, only events well spaced in arrival time from their predecessors have precise energy measurements. We define these high-resolution events to include high-resolution primary (Hp) and medium-resolution primary (Mp) for a total Hp+Mp rate. As the count rate in a pixel increases, the Hp+Mp yield does too until the average time delay between arriving photons becomes shorter than the length of the high-resolution optimal filtering template (Section 5.3). Above this, the fraction of Hp+Mp events monotonically decreases, although this is counterbalanced up to a point by higher total count rates. For point-like sources the events are distributed unevenly across the array and the total array Hp+Mp rate,
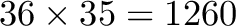 , depends on the total source flux, the shape of the PSF and pointing center relative to the center of the Resolve array, and the source spectrum.
, depends on the total source flux, the shape of the PSF and pointing center relative to the center of the Resolve array, and the source spectrum.
 reaches a maximum of
reaches a maximum of  100 counts s
100 counts s for an on-axis point source at a total incident rate of 1000 counts s
for an on-axis point source at a total incident rate of 1000 counts s on the array, but this theoretical maximum far exceeds the ability to process events (see next section).
on the array, but this theoretical maximum far exceeds the ability to process events (see next section).
While the maximum Hp+Mp rate for a point source occurs at a total count rate of  1000 counts s
1000 counts s , the Pulse-Shape Processor (PSP) can only process about 200 counts s
, the Pulse-Shape Processor (PSP) can only process about 200 counts s for an on-axis source (Mizumoto et al. , 2025a). The PSP houses four CPUs, one for each quadrant of the Resolve array, so the limit is actually 50 counts s
for an on-axis source (Mizumoto et al. , 2025a). The PSP houses four CPUs, one for each quadrant of the Resolve array, so the limit is actually 50 counts s per quadrant, with the 200 counts s
per quadrant, with the 200 counts s assuming an even distribution of counts between the quadrants. Above this rate, some events are not processed by the PSP and are instead recorded as “lost.”
assuming an even distribution of counts between the quadrants. Above this rate, some events are not processed by the PSP and are instead recorded as “lost.”
Events are lost when they arrive too fast for the processor to handle. Here we summarize the PSP operation. The signal from each pixel is digitized and events are identified as pulses in a field-programmable gate array (FPGA) board. When an event is detected, the time series containing the event data (whose length depends on the event grade; Section 5.3.3) is stored in memory and the record of the event is passed to one of the PSP computers, which maintains a list of events waiting to be processed. Events are processed by retrieving the event data from the memory buffer and applying optimal filtering (cross correlation with an optimal template) to measure the event energy and search recursively for secondary events. The pulse height, arrival time, and other data are then sent to the data recorder, the buffer memory occupied by that event is freed, and the computer retrieves the next event. When events fill the buffer faster than the PSP can process them, to make space for new events the entire buffer is cleared and those events are recorded as lost. There is a record of lost events from the FPGA, but their energies are not measured by the PSP and the FPGA count rate is a lower limit as no secondary event search is performed. Note that event loss is independent of energy or grade.
Another form of event loss is analogous to pile-up in X-ray CCD detectors. When two events arrive within 2 ms they are erroneously treated as a single event. Most, but not all, such events are identifiable via anomalous RISE_TIME and SLOPE_DIFFER behavior and are screened out. At high count rates, several percent of the events can be lost this way (Mizumoto et al. , 2025a).
Electrical cross-talk can degrade the energy resolution (Section 5.3.6). In general, cross-talk must be taken into account for velocity measurements that are nearly limited by the instrumental resolution even without cross-talk in sources with 2-10 keV
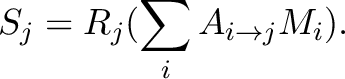 erg s
erg s cm
cm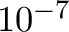 .
.
![\begin{figure}\centering
\includegraphics[width=1\textwidth]{Figures_Bright_Source/crosstalk1.pdf}
\end{figure}](img139.gif) |
Cross-talk occurs because of capacitative coupling between adjacent wires: an event in one pixel produces a voltage pulse (the “parent”) that induces a smaller “child” pulse in neighboring wires. There is also thermal cross-talk, but it is an order of magnitude weaker. The amplitude of the child pulses is 0.6% of the parent for neighboring wires and 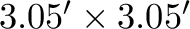 0.1% for next-nearest wires. Due to the wiring map of the array, child pulses are not necessarily induced in physically adjacent pixels (Figure 8.1). Most pixels produce two child pulses per parent, and several produce only one.
0.1% for next-nearest wires. Due to the wiring map of the array, child pulses are not necessarily induced in physically adjacent pixels (Figure 8.1). Most pixels produce two child pulses per parent, and several produce only one.
Most child pulses are below the event detection threshold, but they do distort the signal. If a child pulse coincides within 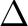 10 ms with the pulse from a real X-ray, the superposition of the two leads to an error in the energy measured from optimal filtering. Such unhappy coincidences naturally increase with count rate. Because errors can be positive or negative, cross-talk effectively degrades the energy resolution. The magnitude of the degradation depends on the incident spectral shape and the count rate. A hard spectrum will produce child pulses with larger average amplitudes than a soft spectrum, and a point source will produce much more cross-talk in some pixels and others.
10 ms with the pulse from a real X-ray, the superposition of the two leads to an error in the energy measured from optimal filtering. Such unhappy coincidences naturally increase with count rate. Because errors can be positive or negative, cross-talk effectively degrades the energy resolution. The magnitude of the degradation depends on the incident spectral shape and the count rate. A hard spectrum will produce child pulses with larger average amplitudes than a soft spectrum, and a point source will produce much more cross-talk in some pixels and others.
![\begin{figure}\centering
\includegraphics[width=1\textwidth]{Figures_Bright_Source/crosstalk2_gvc.pdf}
\end{figure}](img140.gif) |
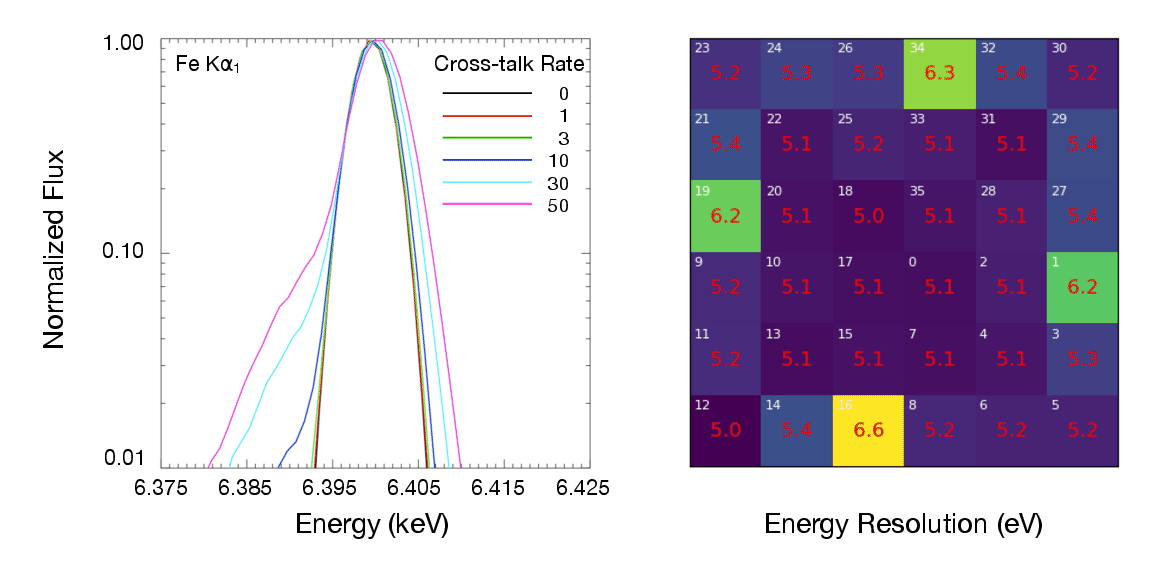
The degradation can be calculated exactly for a monochromatic source and a given pixel, but for a physically motivated spectral model and a full array we must calculate it statistically. The coupling between wire pairs is not uniform across the array, and the optimal filter also differs for each pixel. Fortunately, tests with ground and on-orbit data for a few Resolve pixels show that this is a minor effect compared to the effect of incident count rate and different spectra. As an illustration, Figure 8.2 shows the impact of cross-talk for a very bright source with 2-10 keV
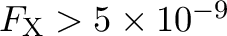 erg s
erg s cm
cm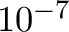 (about 4 Crab), assuming an on-axis point source with a Crab-like spectrum plus a Fe K
(about 4 Crab), assuming an on-axis point source with a Crab-like spectrum plus a Fe K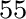 line and no filters. The left panel shows the broadening and centroid shift at Fe K
line and no filters. The left panel shows the broadening and centroid shift at Fe K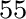 with this spectrum. The right panel shows the average energy resolution in each pixel, starting from a fiducial 5 eV resolution. The pixel pattern results from the shape of the PSF and the wiring map. More examples of the impact of cross-talk on energy resolution are given for simulated spectra in Mizumoto et al. (2025a). Finally, since cross-talk depends on the incident count rate it the energy resolution degradation can be time variable, e.g., for a bursty source the resolution may degrade and centroids shift during the burst.
with this spectrum. The right panel shows the average energy resolution in each pixel, starting from a fiducial 5 eV resolution. The pixel pattern results from the shape of the PSF and the wiring map. More examples of the impact of cross-talk on energy resolution are given for simulated spectra in Mizumoto et al. (2025a). Finally, since cross-talk depends on the incident count rate it the energy resolution degradation can be time variable, e.g., for a bursty source the resolution may degrade and centroids shift during the burst.
Because cross-talk occurs on an event-by-event basis it can be mitigated or removed by screening out affected events, i.e., those in electrically neighboring pixels that occur within the 10 ms coincidence window. The Resolve pipeline software automatically flags, but does not exclude, such events, allowing users to filter the spectrum by STATUS flags. At very high count rates, this filtering can exclude a large fraction of events, especially in the worst-affected pixels. However, with the gate valve closed few sources are bright enough for filtering to significantly affect the amount of “good” time.
Energy flux from bright sources can lead to a systematic negative shift ( 1 eV) in the measured energy of incident X-rays (Mizumoto et al. , 2025b). The gain, used to define the energy scale for measured pulse heights, is a function of pixel temperature (which slowly increases over time between cycles of the adiabatic demagnitization refrigerator) and is tracked during Resolve observations with
1 eV) in the measured energy of incident X-rays (Mizumoto et al. , 2025b). The gain, used to define the energy scale for measured pulse heights, is a function of pixel temperature (which slowly increases over time between cycles of the adiabatic demagnitization refrigerator) and is tracked during Resolve observations with 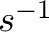 Fe measurements. The detector frame, which serves as a heat sink for the detector pixels, is locally heated by incoming photons. For large energy flux, the pixel temperatures depart from the fiducial value used to calculate the energy scale so that photon energies measured from these pixels will have a negative energy offset.
Fe measurements. The detector frame, which serves as a heat sink for the detector pixels, is locally heated by incoming photons. For large energy flux, the pixel temperatures depart from the fiducial value used to calculate the energy scale so that photon energies measured from these pixels will have a negative energy offset.
Figure 8.3, left panel, shows the energy offset as a function of the total incident energy flux. The plot includes results from both ground-based tests (Mizumoto et al. , 2025a) and in-flight measurements using the Crab Nebula (Mizumoto et al. , 2025b). Although there is considerable scatter in the data, these measurements can be used to estimate the energy shift. For an incoming rate of 10–15 counts s pix
pix and an average photon energy of 5.3 keV (as observed in the central four pixels from the GX 13
and an average photon energy of 5.3 keV (as observed in the central four pixels from the GX 13 1 observation during the Performance Verification phase), the energy flux is
1 observation during the Performance Verification phase), the energy flux is  50–80 keV s
50–80 keV s pix
pix and we expect an offset of about
and we expect an offset of about 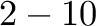 eV as shown in the right panel of Figure 8.3 (Mizumoto et al. , 2025b). Because of the PSF pattern, the energy shift varies across the array.
eV as shown in the right panel of Figure 8.3 (Mizumoto et al. , 2025b). Because of the PSF pattern, the energy shift varies across the array.
![\includegraphics[width=1\textwidth]{Figures_Bright_Source/EnergyShift_BrightSource.pdf}](img143.gif)
|
Typically, observers should aim to maximize the “clean” Hp+Mp rate, i.e., the rate of events with acceptable resolution degradation or gain shift for the scientific goal. Energy resolution begins to degrade above 0.3-10 keV
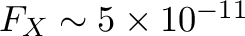 erg s
erg s cm
cm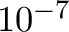 and becomes important to common analyses at
and becomes important to common analyses at 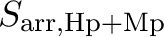 erg s
erg s cm
cm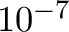 . Event loss becomes important around the same flux level.
. Event loss becomes important around the same flux level.
| Flux | No filter | ND Filter | ND+Off-axis | ||||||
(0.3-10 keV 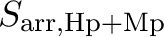 |
Total | Hp+Mp | Clean | Total | Hp+Mp | Clean | Total | Hp+Mp | Clean |
erg s cm cm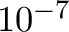 ) ) |
(ph s ) ) |
(ph s ) ) |
(ph s ) ) |
||||||
| 0.5 | 35 | 30 | 15 | 10 | 10 | 5 | 10 | 10 | 5 |
| 1.0 | 70 | 45 | 30 | 20 | 15 | 5 | 20 | 15 | 10 |
| 2.0 | 140 | 60 | 50 | 30 | 30 | 15 | 30 | 25 | 20 |
| 3.0 | 210 | 70 | 50 | 50 | 35 | 15 | 50 | 35 | 25 |
| 4.0 | 280 | 70 | 50 | 70 | 45 | 30 | 60 | 40 | 25 |
| 5.0 | 350 | 80 | 45 | 90 | 50 | 30 | 80 | 40 | 30 |
| 6.0 | 420 | 85 | 40 | 100 | 50 | 45 | 100 | 40 | 25 |
| 7.0 | 490 | 85 | 30 | 120 | 60 | 45 | 110 | 50 | 25 |
| 8.0 | 560 | 80 | 25 | 140 | 60 | 45 | 130 | 50 | 25 |
| 9.0 | 630 | 80 | 25 | 160 | 65 | 50 | 150 | 50 | 25 |
| 10. | 700 | 80 | 10 | 170 | 70 | 55 | 160 | 50 | 30 |
| 20. | 1410 | 70 | 1 | 340 | 80 | 40 | 330 | 65 | 30 |
| 50. | 3520 | 30 | 0 | 860 | 80 | 5 | 810 | 65 | 35 |
Values assume an on-axis source except for the “off-axis” set at a fiducial offset of  0.5 arcmin offset in both DETX and DETY. “Clean” events have an average energy resolution within 2% of a fiducial 5 eV. Bold text indicates the rate for the optimal configuration. The input spectrum is a 0.5 arcmin offset in both DETX and DETY. “Clean” events have an average energy resolution within 2% of a fiducial 5 eV. Bold text indicates the rate for the optimal configuration. The input spectrum is a 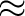 power law with photoelectric absorption from power law with photoelectric absorption from 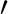 cm cm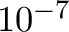 of foreground atomic gas. Exact values are sensitive to the spectrum and other factors. This table is for illustration only. of foreground atomic gas. Exact values are sensitive to the spectrum and other factors. This table is for illustration only.
|
|||||||||
Above this threshold, maximizing the clean Hp+Mp rate is achieved by reducing the incident count rate relative to an on-axis point source. This can be done by observing through a filter (Figure 8.4), placing the target off-axis, or both. The neutral density filter reduces the count rate at every energy by a factor of about four, while the beryllium (Be) filter removes most photons below 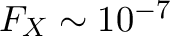 keV. The Be filter is redundant with the gate valve, which has a Be window thicker than the Be filter. For an example XRISM observation (of Cyg X-1) that used the neutral density filter, see Yamada et al. (2025), resulting in a spectrum dominated by clean Hp events with 15 counts s
keV. The Be filter is redundant with the gate valve, which has a Be window thicker than the Be filter. For an example XRISM observation (of Cyg X-1) that used the neutral density filter, see Yamada et al. (2025), resulting in a spectrum dominated by clean Hp events with 15 counts s over the array.
over the array.
Off-axis pointing reduces the count rate by causing more focused X-rays to fall off the chip, and can also be used to concentrate low-resolution events and their cross-talk signals in one sacrificial quadrant. Figure 8.5 illustrates this for a Crab-like point source placed diagonally opposite the quadrant with the calibration pixel. The upper right quadrant is dominated by low-resolution events and contributes 10% of the Hp+Mp events, whose energy resolution is also degraded by up to 2.5 eV. However, the other three quadrants yield 55 counts s with an expected energy resolution within 0.1 eV of the fiducial 5 eV value. Please note that this is not a high fidelity simulation: it does not include the effect of gain shift nor pixel-to-pixel wiring or template differences, and the sharp edges of the PSF can change the count rate distribution compared to the prediction from the xrtraytrace tool. However, most of these effects are concentrated in the sacrificial quadrant, so one can still estimate whether off-axis pointing is useful.
with an expected energy resolution within 0.1 eV of the fiducial 5 eV value. Please note that this is not a high fidelity simulation: it does not include the effect of gain shift nor pixel-to-pixel wiring or template differences, and the sharp edges of the PSF can change the count rate distribution compared to the prediction from the xrtraytrace tool. However, most of these effects are concentrated in the sacrificial quadrant, so one can still estimate whether off-axis pointing is useful.
![\includegraphics[width=0.6\textwidth]{Figures_Resolve/resolve_effective_area_filters_xlog_CVC.pdf}](img149.gif)
|
Thus, Table 8.1 illustrates how the optimal configuration (in bold) changes with increasing count rate for a Crab-like spectrum. For sources brighter than
 erg s
erg s cm
cm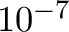 , the ND filter becomes optimal. Above
, the ND filter becomes optimal. Above
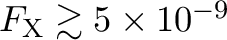 erg s
erg s cm
cm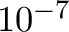 , off-axis pointing is also necessary. The numbers in this table are provided as a guide, but for source fluxes near a threshold, users should carefully balance the observing strategy and proposed exposure time.
, off-axis pointing is also necessary. The numbers in this table are provided as a guide, but for source fluxes near a threshold, users should carefully balance the observing strategy and proposed exposure time.
Table 8.2 summarizes general recommendations as a function of source brightness. To estimate the count rate for a spectrum of interest, proposers should use the spectral responses provided with a simulated spectrum (e.g., via WebPIMMS:
https://heasarc.gsfc.nasa.gov/cgi-bin/Tools/w3pimms/w3pimms.pl). On-axis, point-source ARFs (which are provided for different filters) are sufficient for this purpose when proposing; there is a small (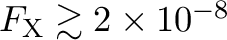 %) decline in effective area for off-axis pointing due to vignetting, but this does not change the optimal strategy.
%) decline in effective area for off-axis pointing due to vignetting, but this does not change the optimal strategy.
While consulting the table is a good first step, proposers should estimate the sensitivity of their scientific goals to energy resolution or scale. If the goal is to measure variable line shifts, broadening in the Fe-K lines at the tens of km s level, or velocity differences between barely resolved absorption lines, proposers should plan to apply the most aggressive event screening and other analysis techniques on the ground, and may wish to pursue more aggressive mitigation in the observing plan or request more exposure time to account for the screening. For example, Yamada et al. (2025) used the neutral density filter for Cyg X-1, resulting in 15 Hp events per second over the array. The table suggests that no filter would produce more Hp+Mp events, but better resolution may be preferable. On the other hand, if an effective resolution of, for example, 5.2 eV does not threaten the science, proposers may wish to maximize the total Hp+Mp count rate and live with the impacts. Finally, we note that when pointing off-axis sources should not be placed in the quadrant with the calibration pixel or the gain cannot be accurately tracked.
level, or velocity differences between barely resolved absorption lines, proposers should plan to apply the most aggressive event screening and other analysis techniques on the ground, and may wish to pursue more aggressive mitigation in the observing plan or request more exposure time to account for the screening. For example, Yamada et al. (2025) used the neutral density filter for Cyg X-1, resulting in 15 Hp events per second over the array. The table suggests that no filter would produce more Hp+Mp events, but better resolution may be preferable. On the other hand, if an effective resolution of, for example, 5.2 eV does not threaten the science, proposers may wish to maximize the total Hp+Mp count rate and live with the impacts. Finally, we note that when pointing off-axis sources should not be placed in the quadrant with the calibration pixel or the gain cannot be accurately tracked.
![\begin{figure}\centering
\includegraphics[width=0.95\textwidth]{Figures_Bright_Source/offaxis_gvc.pdf}
\end{figure}](img153.gif) |
The challenges listed above, and several others, affect data analysis (for a primer on data analysis, see https://heasarc.gsfc.nasa.gov/docs/xrism/analysis/abc_guide/xrism_abc.pdf). It is beyond the scope of this document to provide analysis recipes for bright sources, but here we list effects to watch out for and briefly describe mitigation.
Secondly, when creating a response for Hp+Mp events the effective area is scaled by the fraction of such events (see Section 5.3.3). On-orbit calibration has found that, for most sources, low-resolution secondary events are not astronomical X-rays but instead background or additional signal produced by an already-detected X-ray. These events are thus ignored in calculating the effective area. However, this is not true for bright sources. There is no definitive prescription to arrive at the correct effective area, but observers can bracket the flux by creating one response assuming all low-resolution secondary events are from the source and another assuming none of them are.
Thirdly, the electron-loss continuum can matter. Response files encode the likelihood that an incident X-ray of a given energy is detected at that energy or any lower energy. If an X-ray is absorbed in the detector pixel but some of its energy is transferred to electrons that scatter out of the pixel, the measured energy will be lower. Since the scattering can remove anywhere from 0% to almost 100% of the X-ray energy, there is a low-level continuum. When using the “medium” or “large” redistribution matrix file for spectral fitting (see Data Reduction Guide), observers may notice that the soft energy band has poor residuals. The extra-large file that includes the electron-loss continuum makes spectral fitting take significantly longer and is primarily used as a final step to check or refine results rather than for initial fitting.
Fourthly, observations during the Performance Verification phase revealed that, in some point sources, the spectrum extracted from the outer ring of Resolve pixels has a modestly different broadband shape from the inner-ring spectrum. The difference does not appear to be explained by dust halos, nor is it clearly from an anomaly in the instrument. As with the other issues with response generation, until this issue is better understood users should expect systematic differences in flux between subarrays or in comparison with other X-ray instruments. This effect does not impact the measurement of line energy or broadening.
The optimal combination of offset pointing and/or filter depends on the source type and science goals. Here we provide basic guidelines for observing point sources of various fluxes with the goal of characterizing Fe K emission or absorption above 6 keV in a source otherwise characterized by an absorbed power law.
| Flux | Recommendation | Clean Rate |
(0.3-10 keV 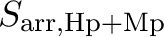 erg s erg s cm cm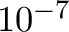 ) ) |
(ph s ) ) |
|
| 0.5-1 | On axis, no filter | 20-30 |
| 1-3 | On-axis, no filter | 40-55 |
| 3-10 | On-axis, ND | 40-60 |
| 10-30 | On-axis (0-0.5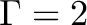 ), ND ), ND |
40-50 |
| 50 | Off-axis (1.0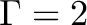 ), ND ), ND |
30 |
“Clean” events are those H+Mp events unaffected by cross-talk, gain shift, or pile-up. The input source is a point source with a a 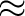 power law spectrum with photoelectric absorption from power law spectrum with photoelectric absorption from 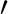 cm cm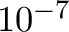 of foreground atomic gas. Exact values are sensitive to the spectrum, structure in the PSF wings, and off-axis position. At all fluxes, the appropriate Xtend mode is 1/8 window of foreground atomic gas. Exact values are sensitive to the spectrum, structure in the PSF wings, and off-axis position. At all fluxes, the appropriate Xtend mode is 1/8 window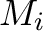 burst, as the source always produces burst, as the source always produces  500 counts s 500 counts s . .
|
||