Accuracy of the GIS Time Assignment
Y. Saito^1, M. Hirayama^1,
T. Kamae^1, H. Kaneda^1,
K. Makishima^1, Y. Sekimoto^1,
N. Kawai^2, T. Dotani^3,
F. Nagase^3, K. Mitsuda^3,
Y. Ishisaki^4, and S. Gunji^5
1 Department of Physics, University of Tokyo,
2 Institute of Physical and Chemical Research (RIKEN),
3 Institute of Space and Astronautical Science,
4 Department of Physics, Tokyo Metropolitan University,
5 Department of Physics, Yamagata University
saito@tkyosf1.phys.s.u-tokyo.ac.jp
1 Introduction
The GIS is designed so as to achieve relative time resolution up to 61
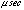when 10 bits are assigned to the time information (Ohashi et al. 1996,
Makishima et al. 1996). Since the absolute timing accuracy also depends on the
stability of the spacecraft clock and the accuracy of the position
determination of the satellite, an in-orbit calibration is necessary.
The calibration status on the GIS time assignment was first reported by
Hirayama et al. (1996), based on the observation of the Crab pulsar and
PSR B1509-58 performed during the PV phase. In that report, they demonstrated
that the absolute accuracy of ASCATIME is better than 2 msec, and the
fractional stability
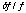is better than
8 x 10-8 s/s on a time scale of about a day, where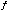 
is the frequency of the on-board
clock oscillator. In this report, after briefly reviewing the time assignment
procedure applied for ASCA, we report more precise values of the absolute
accuracy and the fractional stability.
The absolute arrival time of an X-ray photon is determined as follows. For an X-ray event, the on-board data processor (DP) latches the on-board scaler, which is calibrated with the ground atomic clock at every down-link (usually five times a day) at Kagoshima Space Center (KSC). The ground clock is calibrated within a few micro seconds of the coordinated universal time (UTC) using Rolan C once or twice a week. The absolute arrival time (ASCATIME) of an X-ray event is determined by interpolating the closest two calibrated times using the value of the on-board scaler. Since the frequency of the on-board clock depends on its temperature, the ASCATIME is further corrected based on the temperature measured every second.
Sources of the inaccuracy of ASCATIME are the transmission delays of
telemetry and the residual temperature dependence of the on-board clock
oscillator. The total systematic error for these is at most 100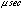 
. Most significant factor
in the former is the uncertainty of the satellite position, measured by
ranging from KSC twice a day. As for the temperature correction, the
fractional stability of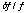 
better than 3 x 10-8 s/s was
achieved for the on-board scaler in the pre-flight test with temperature
drift of 10 degrees in 8 hours. In addition, the accuracy is further
limited by the GIS time resolution less than 61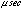 
and the truncation to the modulo of 100 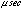at the calibration of the
on-board scaler to the ground clock.
2 Observation
In the middle of September 1996, we observed three pulsars, the Crab pulsar, PSR B1821-24 (Saito et al. 1997), and PSR B1509-58 as listed in table 1. The GIS telemetry mode was set to high time resolution mode. To avoid dead time due to the high counting rate of the Crab nebula, it was placed 17 mm (17 arcmin) off-axis, and the GIS lower-level discriminator was set to the highest level (~3.3 keV for this particular offset position). The resultant counting rates for the Crab nebula were 52 c/s for GIS2 and 68 c/s for GIS3, which cause dead times of ~ 10%. We summarize the observation log in figure 1.
Table 1: Observation for timing calibration and the GIS operation mode.
3 Analysis and Results
We used the GIS data for following analysis. The first correction in the
analysis is removal of the systematic offset of the photon arrival times
assigned by the standard analysis package. Second, we removed the systematic
offset of -50
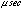introduced by the finite (100
)
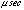resolution of the time assignment at KSC. Then, the arrival time of each
photon is shifted by half the GIS time resolution specified by the number of
the telemetry timing bit. It is necessary because the epoch of the leading
boundary of a time bin is defined as the photon arrival time instead of the
central epoch of the time bin
Figure 1: Time table of the observations for timing calibration performed in September 1996. Arrows indicate the times when daily calibration of on-board scaler with the atomic clock at KSC was performed.
Photon arrival times are further converted to those at the solar system
barycenter, and then folded at the predicted pulse period of each pulsar using
the radio ephemeris listed in table 2. The absolute timing accuracy of the
radio ephemerides are 100
. We used events
collected with the earth elevation angle higher than
5 degrees, and within 3 arcmin from PSR B1509-58 and
PSR B1821-24. We used photons corrected in the entire field of view to analyze
the Crab data.
3.1 Absolute Time
Figure 2 shows pulse profiles obtained from PSR B1509-58 and the Crab #1. The dashed lines are the expected peak phases. For PSR B1509-58, it is 0.25 phase after the radio peak with an error of 0.02 phase shown by dotted lines (Kawai et al. 1991). For the Crab pulsar it is the phase of the radio main peak after removing the dispersion due to interstellar medium. Results from GIS2 and GIS3 are in a good agreement. In addition, the observed pulse peak phases are in reasonable agreement with the prediction, indicating that the accuracy of ASCATIME is at least better than the peak width of the Crab pulsar.
Figure 3 shows expansion of the main peak phase of Crab #1, Crab #2-3, and
Crab #2-2 observations. The peaks of the data obtained at Crab #2-2 are not
sharp, since they are obtained in the MPC mode with only 1.95 msec (~ 0.06
phase of the Crab) time resolution. The peak phase was determined by fitting
the light curve with Gaussian + linear background. The offsets are shown at the
bottom of each figure with 90% errors including the systematic error of 30
for using the Gaussian as the model pulse shape.
Figure 2 Pulse profiles of PSR B1509-58 (a and b) and the Crab #1 (c and d). The dashed lines are the expected peak phases. The dotted lines in (a) and (b) show the uncertainty in the predicted peak phases. The observed phases are in reasonable agreement with the prediction.
Figure 3 Pulse profiles of the Crab pulsar around the first peak for Crab #1 (PH mode; panels a and b), Crab #2-3 (PH mode; panels c and d), and Crab #2-2 (MPC mode; panel e and f). The dashed lines are the expected peak phases with errors indicated by dotted lines. Offsets of the X-ray peaks from the radio peaks are shown with 90% errors at the bottom of figures.
The Craba PSR B1821-24a PSR B1509-58b
Right Ascension 83.63322 276.13337 228.48178
(J2000)
Declination (J2000) 22.01446 -24.86976 -59.13598
t0c (MJD) 50340.0 50215.0 50205.0
Phase at t0d 0.712 0.98 0.6317
f0 (S-1)c 29.8851774605799 327.4056597973296 6.6267743270631
f1 (S-2)c -3.75684 x 10-10 -1.l73520 x 10-13 -6.73824 x 10-11
f2 (S-3)c 2.09 x 10-20 0.00 1.95 x 10-21
We found that the X-ray peaks obtained both with PH mode and MPC mode are
almost aligned to those of the radio peaks within errors of 200
.
It is also apparent that the peak "moved" during the three observations (note
that the 100
uncertainty in the peak phase of the radio ephemeris is a systematic offset and
is common to all the three observations). The errors in peak phases are
considered to be mainly from this drift, since the systematic errors for the
absolute time is at most less than 100
.
Stability of the clock will be discussed in following section.
3.2 Fractional Stability
The stability of ASCATIME is studied below from five aspects. Since GIS2 and GIS3 gave consistent results, we combined them in the following analysis.
The stability on one day time scale was derived from the drift of the X-ray
peak phase between Crab #1 and Crab #2-3. The integrated fractional stability
for a time span of 30 hr i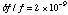s
s/s.
For the study of the stability on shorter time scales, we subdivided each of
the Crab #1 and Crab #2 data into three non-overlapping data segments separated
typically by ~ 100 min (the spacecraft orbital period) and made pulse profiles
around the first peak phase as shown in figure 4. In either cases, the peak
drifts by ~ 100
during the observation span of ~ 10 ksec so that we find the fractional
stability of ASCATIME on this time scale to be
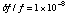s/s.
Figure 4 Pulse profile of the Crab pulsar around the first peak obtained from three time segments. (a) Crab #1. Top is 21:15 ~ 21:50 (2.1 ksec), middle is 23:00 ~ 23:50 (3.0 ksec), and bottom is 0:25 ~ 1:10 (2.7 ksec). (b) Crab #2-1, and #2-3.
Top is 0:40 ~ 1:25 (2.6 ksec), middle is 5:15 ~ 6:15 (1.3 ksec), and bottom is 6:45 ~7:45 (1.6 ksec).
The stability is also studied by the analysis of the millisecond pulsar
PSR B1821-24, from which double-peaked hard X-ray pulsation was recently found
(Saito et al. 1997). Figure 5 shows the 48 phase-bin periodgram of
PSR B1821-24 using the whole observation span, with an arrow indicating the
period expected from the radio ephemeris. The expected period is 3.054314963
msec, while the obtained peaked period was 3.054314971
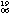msec (errors are for last two digits). The disagreement in the pulse period (
1 x 10-9 msec) may be regarded as the fractional error of
ASCATIME
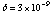during the observation span of ~ 67 ksec.
The drift of ASCATIME on a time scale of the satellite orbital period (~ 100
min) is also studied using this pulsar. Figure 6 shows the pulse profiles of
48 phase bin for two cycles obtained at three different time spans. We used
the averaged pulse period determined over the whole observation to fold the
individual datasets. The phase shift due to period derivative is known to be
negligible. During the time for the middle data set, the satellite was in the
visible orbit from KSC. The significant shift of the pulse phase by 0.3 msec
from top to middle indicate a fractional stability of
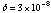s/s on a time span of ~ 11 ksec.
The stability on the same time scale can be further estimated from the pulse
width of PSR B1821-24. It is known that one of the two peaks is very narrow
(Saito et al. 1997). Although we do not know its intrinsic width, we can use
the observed width to estimate the upper limit on the clock stability assuming
an infinitesimal width. The FWHM of the narrow peak in figure 6 is 3 bins,
corresponding to 0.2 msec. We thus obtain a fractional stability of
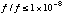s/s over ~14 ksec integration.
Figure 5 Periodgram of 48
phase-bin for PSR B1821-24 using the whole observation span of 67 ksec.
The peaked period of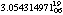 
msec (errors are for last two digits) which
is slightly different from the expected period (3.054314963 msec)
indicated by an arrow. The error is estimated from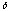 
;
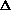Red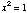
.
It is to be noted that the fractional clock error determined from the pulse phase shift of PSR B1821-24 is larger than those on similar time scales determined by the pulse width of PSR B1821-24 and the phase shift of the Crab pulse. In particular, comparing the three pulse profiles of PSR B1821-24, we find that the pulse profiles are sharper in two latter data sets, and the phase shift is only seen from the first data set to the second data set. This is most reasonably explained by the incompleteness of the temperature compensation for the first data set. As shown in figure 1, the correction of the on-board clock for the first data set is based on the two calibrations separated by 41 hours, much longer than the calibration intervals for the other data sets, and is likely to have larger errors in the clock correction.
Figure 6 Pulse profiles of PSR B1821-24 obtained at three time spans. Top is 2:50 ~ 7:10 (8.6 ksec), middle is 7:40 ~ 15:00 (14.2ksec), and bottom is 15:50 ~ 18:20 (7.0 ksec).
4 Summary
Based on the observations of three pulsars, the Crab pulsar,
PSR B1509-58, and PSR B1821-24, we studied the accuracy of the ASCA
time assignment. From comparison of the GIS data of the Crab pulsar and
PSR B1509-58 with the radio ephemerides, we confirmed that the absolute
accuracy of the GIS time assignment is better than 200
for
both the PH mode and the MPC mode, from the alignment of the X-ray peak and the
radio peak of the Crab pulsar.
We summarized the fractional stability of ASCATIME as a function of measurement
interval in figure 7, together with those of the on-board clock and the ground
atomic clock at KSC. The fractional stability of ASCATIME is affected by the
uncertainty of the various factors of the GIS time assignment, such as of the
residual temperature-dependent drift of the on-board clock, the uncertainty of
the satellite position, and the truncation to the finite time resolution of the
GIS and the calibration of the on-board scaler with UTC. The fractional
stability of ASCATIME on a time scale of T can be roughly described as
.
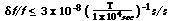5 Acknowledgment
We thank Prof. A.G. Lyne and Dr. V.M. Kaspi for providing the precise radio ephemerides.
6 Reference
Ohashi, T. et al. 1996, PASJ, 48, 157.
Makishima, K. et al. 1996, PASJ, 48, 171.
Hirayama, M. 1996, ASCANEWS, No.4, 18.
Lyne, A. G. 1996, Private communication.
Kaspi, V. M. 1996, Private communication.
Kawai, N. et al. 1991, ApJ, 383, L65.
Saito, Y. et al. 1997, ApJ Let. to appear in March 1 issue.
Figure 7 Stability of ASCATIME.
Proceed to the next article
Return to the previous article
Select another article