compTT: Comptonization, Titarchuk
This is an analytic model describing Comptonization of soft photons in
a hot plasma, developed by Titarchuk (see Titarchuk 1994, ApJ 434, 313). This
replaces the Sunyaev-Titarchuk Comptonization model (compST)
in the sense that
the theory is extended to include relativistic effects. Also, the
approximations used in the model work well for both the optically thin
and thick regimes. The Comptonized spectrum is determined completely
by the plasma temperature and the so-called  parameter which is
independent of geometry. The optical depth is then determined as a
function of parameter which is
independent of geometry. The optical depth is then determined as a
function of  for a given geometry. Thus par5 switches
between spherical and disk geometries so that for a given geometry. Thus par5 switches
between spherical and disk geometries so that  is not a direct
input here. This parameter MUST be frozen. If par5 is not a direct
input here. This parameter MUST be frozen. If par5 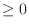 , ,
 is obtained from the optical depth using analytic
approximation (e.g. Titarchuk 1994). If par5 <0 and is obtained from the optical depth using analytic
approximation (e.g. Titarchuk 1994). If par5 <0 and
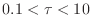 , ,  is obtained by interpolation from a set of
accurately calculated pairs of is obtained by interpolation from a set of
accurately calculated pairs of  and and 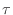 from Sunyaev &
Titarchuk (1985, A&A 143, 374). from Sunyaev &
Titarchuk (1985, A&A 143, 374).
In this incarnation of the model, the soft photon input spectrum is a
Wien law [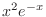 photons] because this lends itself to a
particularly simple analytical form of the model. For present X-ray
detectors this should be adequate. Note that in energy flux space the
peak of the Wien law occurs at 3kT as opposed to 2.8kT for a
blackbody. The plasma temperature may range from 2-500 keV, but the
model is not valid for simultaneously low temperatures and low optical
depth, or for high temperatures and high optical depth. The user is
strongly urged to read the following references (esp. HT95 Fig 7)
before and after using this model in order to fully understand and
appreciate the physical assumptions made: Titarchuk (1994, ApJ
434,
313);
Hua & Titarchuk (1995, ApJ 449, 188);
Titarchuk & Lyubarskij (1995, ApJ 450, 876). photons] because this lends itself to a
particularly simple analytical form of the model. For present X-ray
detectors this should be adequate. Note that in energy flux space the
peak of the Wien law occurs at 3kT as opposed to 2.8kT for a
blackbody. The plasma temperature may range from 2-500 keV, but the
model is not valid for simultaneously low temperatures and low optical
depth, or for high temperatures and high optical depth. The user is
strongly urged to read the following references (esp. HT95 Fig 7)
before and after using this model in order to fully understand and
appreciate the physical assumptions made: Titarchuk (1994, ApJ
434,
313);
Hua & Titarchuk (1995, ApJ 449, 188);
Titarchuk & Lyubarskij (1995, ApJ 450, 876).
| par1 |
Redshift |
| par2 |
Input soft photon (Wien) temperature (keV) |
| par3 |
Plasma temperature (keV) |
| par4 |
Plasma optical depth |
| par5 |
Geometry switch. (sign denotes approximation technique,
magnitude determines geometry). 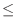 1 disk, >1 sphere, 0
use analytic approximation for 1 disk, >1 sphere, 0
use analytic approximation for  vs. vs. 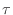 , <0 , <0  vs.
vs. 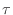 from interpolation. from interpolation. |
| norm |
normalization |
HEASARC Home |
Observatories |
Archive |
Calibration |
Software |
Tools |
Students/Teachers/Public
Last modified: Tuesday, 28-May-2024 10:09:22 EDT
|

