NOTICE: This Legacy journal article was published in Volume 2, November 1992, and has not been updated since publication. Please use the search facility above to find regularly-updated information about this topic elsewhere on the HEASARC site.

ROSAT PSPC

Günther Hasinger (MPE), T. Jane Turner (GSFC ROSAT GOF),
Ian M George (HEASARC) & Günter Boese (MPE)

---

	Version: 1992 Oct 05	OGIP Calibration Memo CAL/ROS/92-001 

Summary

The components of the ROSAT PSPC on-axis point spread function (p.s.f.) are discussed, and a direct comparison made between the predicted p.s.f. from ground calibration measurements and in-flight data obtained during the early part of the mission. It is found that the analytical functions derived from the ground calibration data satisfactorily describe the 5 in-flight datasets tested here.

It should be noted that this is not intended to be the definitive write-up of the PSPC p.s.f. Rather, the aim of the memo is to distribute the currently available information to ROSAT PIs in a timely fashion. The author list does not reflect the input of all the people involved with the PANTER data. It is expected that a full write-up will appear at a later date.

1 Introduction

The p.s.f. of the ROSAT X-ray mirror assembly (XMA) + PSPC is a convolution of several components:

The XMA scattering profile

The off-axis blur of the XMA

The intrinsic spatial resolution of the PSPC

Focus and detector penetration effects

A widening of the PSPC resolution due to the existence of 'Ghost images' (for PHA channels < 20 only)

The Ellipsoidal blur due to residual attitude motion

These are individually discussed in more detail below. Specifically the on-axis p.s.f. is described in detail, comparing the form derived from an analysis of ground calibration data with that obtained in orbit. The off-axis p.s.f. will be discussed in more detail in a future OGIP calibration memo.

Throughout,
is the off-axis angle (in arcmin) from the center of the PSPC field of view,
r is the radius (in arcmin) from the p.s.f. centroid,
PSF(E,r) is the p.s.f. (in normalized cts area^-1),
and E is the photon energy (in keV).

1.1 The XMA Scattering Profile

Microroughness of the reflecting mirror surfaces leads to non-specular reflection of X-rays, i.e., scattering. Theoretically, assuming the grazing angle remains constant, the scattering fraction should increase as E². Due to the laws of diffraction, the shape parameters should be 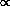E^-1.

The importance of scattering by the ROSAT XMA is small compared to previously available X-ray mirrors, offering the ability to perform high contrast imaging. The form of the scattering is a complex function of energy, grazing angle and the scale size of the mirror surface roughness. The combination of these effects can be modelled as a Lorentzian which breaks to a power law at high radii.

1.2 The Off-axis Blur of the XMA

The off-axis p.s.f. of grazing incidence optics is rather complicated. A convenient measure of the image spread is the so-called RMS blur radius, defined as the radius within which 68% of the photons fall, i.e., the Gaussian sigma of the distribution of photons for a given off-axis angle. The expected ROSAT XMA rms blur circle radius, rblur, increases rapidly with off axis angle. The off-axis effects will be treated in a subsequent p.s.f. memo.

1.3 The Intrinsic Resolution of the Counter

Due to the inherent statistics of the primary electron generation, the intrinsic spatial resolution of the ROSAT PSPC is expected to be a Gaussian. Theoretically its width is 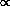E ^-1/2 and independent of .

1.4 Focus and Penetration Effects

The design distance between the XMA and PSPC (the window of which is flat) is such that photons of ~1 keV on-axis source are brought to a focus (along a surface of a cone of half-angle 8.5° ) at an optimum depth within the PSPC drift region such that the Gaussian spatial distribution of pulses on the cathode wires is minimized. Consequently the image of a point source is sharpest at 1 keV.

1.5 Ghost Images

The position of an event in the PSPC is determined from the amplitudes of signals on the two cathode grids. The specific algorithm uses the two highest signals from each cathode grid (the cathode grids are divided into something like 22 segments with separate amplifiers). For events with large pulse-height amplitudes, this works very well since the strength of the signals on the cathode segments is related to the strength of the signal on the anode. However, for small pulse-height amplitudes, occasionally only one cathode segment of a grid will have a signal above the lower discriminator. This still gives a well specified, but incorrect, position. If two segments of one grid have signals but only one of the segments from the other grid has a signal, then the determined position will lie along a line. If only one segment from each grid has a signal, then the determined position will lie at a point. This structure is very apparent when looking at an image of events in detector coordinates with pulse heights less than channel 15 (~ 0.15 keV). There is a cross-work pattern of lines with bright spots at the intersections. There are secondary bright spots in the centers between the lines since the probability is greater there to get signals on four cathodes.

1.6 Ellipsoidal blur due to residual attitude motion

Generally, SASS processing allows only data of good attitude solution to be included in the "Good-Time Intervals" (GTIs). Only data with attitude solutions better than ~2 arcsec are included in the GTIs for sequences processed by SASS after 1991 Dec (earlier processing had a looser constraint on the attitude solution, sometimes resulting in a noticeable asymmetric blurring of the image).

2 Ground Calibration Data

The detailed p.s.f. parameters and their associated E dependences have been determined for PSPC-A & PSPC-C using 4 monochromatic energies (0.28, 0.93, 1.49 & 1.70 keV) at the PANTER test facility in Garching.

Currently, results for three of the components of the p.s.f. have been determined -- namely the PSPC intrinsic resolution, focus and penetration effects and the effects due to mirror scattering. In principle the resultant three components should be folded with each other, however, they are sufficiently well separated in the r (spatial) domain that MPE considers a simple addition accurate enough.

2.1 The XMA Scattering Profile

The analytical form derived for the fraction of photons within this component as a function of energy is given by:

               Fscatt = 0.059 E+1.43                (1)

It can be seen from Figure 1 that even at high energies F_scatt is small compared to the other components. The model and the PANTER data from which eqn 1 was derived are also shown in Figure 2. The increase in F_scatt with E is slower than the E² powerlaw expected due to the detailed structure (micro-roughness) of the mirror surface.

The PANTER tests confirmed that this component was well approximated by a Lorentzian, as expected (Section 1.1), steepening to a powerlaw at large r, i.e.,

                     PSFscatt(E,r) =  for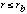 
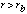                                = PSF(E,rb) (r/rb)- for 				(2)

where

	              rb(E) = 861.9/60 E-1 arcmin       (3)

and

	              = 2.119 + 0.212E       		      (4)

The width of the Lorentzian, r_scatt(E), as a function of energy was found to be:

	              rscatt(E) = 79.9/60 E-1 arcmin     (5)

and is plotted in Figure 3. The two parameters governing the shape of PSF_scatt(E) (i.e., r_b and r_scatt) were constrained to be proportional to E^-1 (see section 1.1) during the analytical fitting to the PANTER data.

The normalization of the Lorentzian, A_scatt,is given by

	            Ascatt = Fscatt(E) /  normalized cts arcmin-2       (6)

where

        = (rscatt/2)2 [ln (1 + (2/rscatt)2 rb2) + 2 rb2 ((rscatt/2)2 + rb2)-1( - 2)-1]       (7)

is the renormalization factor such that[1]

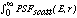               2r dr  = Fscatt(E)       (8)

A_scatt is plotted as a function of E in Figure 4.

The fraction of incident photons scattered outside a radius, r_cell, is shown as a function of energy for various r_cell in Figure 5. It should noted that at 1 keV, ~ 6% of incident photons will be scattered outside r_cell = 100 arcsec, and ~ 5% outside r_cell = 10 arcmin.

To summarize:

At low energies, the strength of this component to the p.s.f. is very small, and its width very large, making it difficult to distinguish this component from the background and/or slow variations in the efficiency of the PSPC. As one moves to higher energies (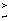 0.5 keV), the strength of the component increases and the width decreases, increasing the importance of this component to the total p.s.f. (see Figure 6).

At energies for which the analytical parameterization of the PANTER data is valid (i.e., 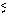2 keV), the steepening from a Lorentzian to a powerlaw form occurs at radii, r_b 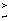10 arcmin. Since the break is relatively gentle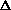 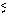0.4), this is unlikely to be detectable in most datasets.

2.2 The Intrinsic Resolution of the PSPC

All photons not in the other 2 components are assumed to be in this component. Thus the fraction of photons within this component as a function of energy is given by:

             Fint = 1 - Fscatt - Fexp                      (9)

As discussed further in Section 2.3, eqn 9 is only valid for E 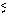2.0 keV as above this energy the derived analytical expression for F_exp implies F_exp > 1 and hence F_int < 0.

The PANTER tests confirmed that this component was well approximated by a Gaussian, as expected from the statistics of the primary electron generation process (Section 1.3); i.e.,

             PSFint(E,r) = Aint(E) exp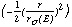 normalized cts arcmin-2  (10)

The derived analytical form for the width of the Gaussian, , as a function of energy is given by:

              = 1/60 ( 108.7 E-0.888 + 1.121E+6)1/2 arcmin    (11)

and is plotted in Figure 3. The model and the PANTER data from which eqn 11 was derived are also shown in Figure 2. It can be seen that decreases and then increases with increasing E within the PSPC band, with a minimum at E 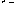1.5 keV. It should be noted that at low energies, the analytical function decreases slightly more slowly with E than the PSF(E) 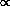E² expected (Section 1.3). For all E within the PSPC energy band, 0.5 arcmin

The normalization, A_int(E), is given by

                Aint(E) = Fint(E) / 2()2) normalized cts arcmin-2			(12)

where the denominator is the renormalization factor such that the integral of PSF_int(E,r) r dr over the range 0 r equals F_int(E). A_int is shown as a function of E in Figure 4.

2.3 Focus and photon penetration effects

The analytical form derived for the fraction of photons within this component as a function of energy is given by:

                   log10Fexp(E) = -1.618 + 0.507E + 0.148E2           (13)

Thus the importance of this component rises relatively quickly with E (Figure 1). The model and the PANTER data from which eqn 13 was derived are also shown in Figure 2. It should be noted that for E 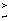2.0 keV, eqn 13 implies F_exp(E) > 1. This is clearly a physically meaningless result, and gives an upper limit on the applicability of the analytical functional forms derived from the PANTER measurements. (The highest photon energy at which the PANTER measurements were carried out was 1.70 keV.)

The combined contribution of focussing and the finite penetration of photons into the counter on the p.s.f. can be is modelled as an exponential function:

          PSFexp(E,r) = Aexp(E)  exp 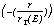 normalized cts arcmin-2   (14)

The e-folding angle, 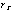, was found to be given by

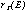                      = 1/60 (50.61 E-1.472 + 6.80 E+5.62)1/2  arcmin         (15)

and is plotted in Figure 3 (see also Figure 2). It can be seen that 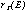is a minimum at E (~,-) 1.1 keV reflecting the fact that the separation between the XMA and PSPC is such that 1 keV photons are brought to a focus at an optimum depth within the counter.

The normalization, A_exp(E), is given by

	      Aexp(E) = Fexp(E)/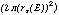 normalized cts arcmin-2    (16)

and as for the other components has been normalized such that the integral of PSF_exp(E,r) r dr over the range 0 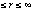equals F_exp(E). A_exp(E) is plotted as a function of E in Figure 4.

To summarize:

The fraction of the photons within this component increases with E (Figure 1); the normalization of the resultant exponential component to the p.s.f. increases with E, then flattens off at ~ 1 keV; whilst the e-folding angle (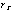) decreases with E for energies below ~ 1 keV, then increases with E at higher energies.

2.4 The Predicted Composite p.s.f.

The predicted composite p.s.f., PSF_tot, for the ROSAT XMA + PSPC combination at a given energy is given by the addition of the components given above (i.e., PSF_scatt + PSF_int + PSF_exp). Examples of PSF_tot are shown in in Figure 6 (solid lines) at several energies, along with curves showing the three individual components. In Figure 7 are shown the corresponding curves of the predicted encircled fraction as a function of radius. For convenience, the radii encircling 50, 90, 95 & 98% of the photons are also listed in Table 1 and plotted in Figure 8. It can be seen that above ~ 1 keV, it is predicted that a substantial fraction (~ 5%) of photons will be scattered by the XMA outside a radius 10 arcmin (see also Figure 5).

                     Table 1:  Encircled Fraction


	              	Energy		Radius (arcmin)
	              	(keV)	50%	90%	95%	98%
			------------------------------------
			0.188	0.44	0.81	0.94	1.14
			0.284	0.36	0.68	0.79	0.99
			0.5	0.29	0.54	0.65	2.20
			1.0	0.22	0.45	1.55	>10
			1.7	0.28	1.36	8.79	>10

In Figure 9, the predicted p.s.f. is compared directly with the PANTER data from which it was derived. It can be seen from the residuals that the fits are generally satisfactory, particularly at radii 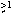arcmin.

It should be emphasized that the above analytical parameterizations are only valid over the energy range 0.15 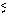E 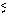2.0 keV (i.e., channels 15-200).

3 The In-flight Data

3.1 Datasets & Extraction

The above Ground Calibration results have been tested against the in-flight datasets listed in Table 2. The letter in parentheses after the ROR number indicates which PSPC was used to obtain the data (PSPC-C was in use prior to its destruction during the sun pointing on 1990 Jan 25). While ideally we would have preferred to use bright calibration sources, many of the sources observed in the first calibration phase are unsuitable for this study. AR LAC was never observed on-axis with the PSPC (in the first calibration datasets) and many of the other calibration targets are extended, often due to the presence of a dust halo. Some satellite maintenance observations which have been made more recently will be used to check these results, but in the meantime we have tested against several point source datasets. Two of the datasets were from the long pointing phase and hence provide excellent signal-to-noise. In any cases where there was some evidence for an extended feature in the point source, or where there were other sources close to the on-axis point source, suitable exclusion regions were set for the profile extraction. Data attitude solutions were checked, and any data with attitude error greater than 2 arcseconds was excluded from the analysis.

Table 2: On-axis In-Flight Datasets

       No.   ROR	     Object	 Class	      Exp (ksec)   Comment
       -------------------------------------------------------------------
       1     rp150071 (C)    NGC5548	 Seyfert 1    18.86	   PV
       2     rp700055 (B)    NGC3998	 LINER	      22.85	   AO1
       3     rp700057 (B)    Pictor A    LINER	      4.46	   AO1
       4     rp700105 (B)    Mkn509	 Seyfert 1    1.77         AO1
       5     rp700104 (B)    ESO141	 Seyfert 1    5.02	   AO1

Radial profiles were extracted using PROS in the five energy bands listed in Table 3. Five was considered optimum for energy resolution with good signal to noise in each band. Typically several thousand counts per source per bandpass were obtained for comparison with the predicted p.s.f.

		Table 3:  The Energy Bands Used

		Name	Energy (keV)	PI Channels
			min	max	min	max
		B	0.10	0.188	9	18
		C	0.188	0.284	19	29
		R1	0.284	0.5	30	50
		R2	0.5	1.0	51	101
		R3	1.0	2.48	102	256

The lowest 8 channels were rejected to exclude problems due to the variable lower limit discriminator for valid events, due to the variable instrument gain which is folded into these data.

The following specifications were applied to the data:

Image centroids were determined, and then radial count profiles were extracted in 5 arcsec increment annuli centered on the centroid position, out to a radius of 5 arcminutes. As the p.s.f. is symmetric on-axis, no information is lost here. The PROS software was used for this extraction.

Any additional sources falling within the specified annuli were masked out of the analysis as noted above.

No background subtraction was carried out. Background rates were measured from the images and were later folded into the predicted profile template for each source in each band. The background count rates are detailed in Table 4, and are generally in good agreement with those expected.

The counts profiles extracted were normalized to counts per square arcminute and the data dumped to ASCII files, suitable for analysis using QDP.

The counts profiles were rebinned such that each spatial bin contained at least 20 photons.

			Table 4:  Results

		No.	ROR	        Bkgd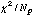		
				        (ct arcmin-2)
	B-band

		1	rp150071 (C)	1.4 x 10^-3	282/27
		2	rp700055 (B)	8.6 x 10^-3	832/39
		3	rp700057 (B)	7.2 x 10^-3	192/9
		4	rp700105 (B) 	1.5 x 10^-3	41/14
		5	rp700104 (B)	3.3 x 10^-3	57/14

	C-band
		1	rp150071 (C)	9.2 x 10^-4	68/22
		2	rp700055 (B)	5.1 x 10^-3	295/36
		3	rp700057 (B)	4.0 x 10^-4	62/13
		4	rp700105 (B)	8.6 x 10^-4	65/15
		5	rp700104 (B)	1.5 x 10^-3	29/17

	R1-band
		1	rp150071 (C)	7.6 x 10^-4	56/19
		2	rp700055 (B)	3.5 x 10^-3	143/26
		3	rp700057 (B)	4.0 x 10^-3	27/12
		4	rp700105 (B)	7.5 x 10^-4	18/12
		5	rp700104 (B)	1.2 x 10^-3	53/16

	R2-band
		1	rp150071 (C)	5.5 x 10^-4	15/17
		2	rp700055 (B)	1.0 x 10^-3	66/24
		3	rp700057 (B)	1.8 x 10^-3	47/16
		4	rp700105 (B)	2.5 x 10^-4	17/12
		5	rp700104 (B)	6.8 x 10^-4	39/20

	R3-band
		1	rp150071 (C)	5.3 x 10^-4	56/22
		2	rp700055 (B)	6.3 x 10^-4	31/22
		3	rp700057 (B)	9.4 x 10^-4	34/15
		4	rp700105 (B)	1.9 x 10^-4	24/14
		5	rp700104 (B)	4.0 x 10^-4	37/19

3.2 Theoretical Curves

The detailed p.s.f. parameters and their energy dependence have been determined using the PANTER telescope calibration data of both PSPC-A and PSPC-C at the monochromatic energies 0.28, 0.93, 1.49 and 1.70 keV. At lower pulseheights than channel 15 (0.15 keV) additional 'ghost images' appear in the PSPC, as described in the previous section, for which no analytical fit is possible. Fits to the B band data are shown to illustrate this point. We will return to this point in the summary.

As the in-flight data are affected by more uncertainties than the ground data (aspect corrections, background subtraction, gain correction etc.) it was not possible to allow profile fitting with the parameters of the Gaussian + exponential + Lorentzian components to be free. Instead we calculated the p.s.f. for every source in each bandpass.

First, a spectrum was extracted for each source, in a circle of size several arcminutes radius (exact region mask used depended on the particular field) to ensure that essentially all of the sources counts were collected. Next, a p.s.f. was calculated for each energy channel. A predicted p.s.f. template was calculated for each dataset using the source spectrum to determine the photon weighting to be applied to the p.s.f. component in each energy channel. Thus for each band and spectrum a combined p.s.f. was produced, including a constant term for the background component from Table 4.

These predicted templates were overlaid on the appropriate datasets as illustrated in Figure 10. As the normalization of the model was also calculated (using the equations in Sections 2.1, 2.2 and 2.3), NO FITTING was performed. The 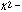statistic for each dataset and band is listed in Table 4. It can be seen that, except in the case of the B band, the model generally gives a good description of the p.s.f. Some slight discrepancies are observed, as can be seen from Figure 10 (particularly the case for NGC 3998). As NGC 3998 is a nearby galaxy, part (or all) the deviation observed in this source may be an indication of genuine extended X-ray emission. This and the fact that no systematic deviations are observed across the other datasets tested leads us to conclude that the p.s.f. model should not be modified based on the NGC 3998 deviations alone. Comparison of more point source datasets should be made before we can determine whether effects such as this should be modelled.

4 Conclusions

The MPE model for the PSPC p.s.f. is good for energies between 0.15 and 2.0 keV. Generally the predicted shape agrees well with the data, with no obvious systematics in any band except the B-band. Thus, within the statistical limits of these datasets, we conclude the model is a satisfactory description of the PSPC p.s.f. More bright source datasets are expected to become available to the ROSAT GOF within the next few months. These may provide a more stringent test of the model, and any discrepancies found will be noted in future OGIP Calibration Memos.

The MPE model does not satisfactorily predict the observed B-band p.s.f. Whilst Figure 10a illustrates the effect of Ghost imaging at low energies, this effect is not (yet) quantifiable. Thus at present, it is recommended that users extract data products within a large enough region such that most the B-band counts are included and a negligible correction is required (see Figure 7 and 8).

Acknowledgements

We thank the many people at MPE involved in the determination & interpretation of the PANTER data, Dave Davis (GSFC) for his help extracting the data and Gail Reichert (GSFC) for supplying some test datasets from her own AO-1 observations.

Figure 1 The fraction of photons in the 3 major components of the ROSAT PSPC on-axis p.s.f. verses photon energy. The functional forms were determined from analytical fits to Ground Calibration measurements on PSPC-A & PSPC-C in the PANTER facility. The fraction of photons within the component due to (1) the intrinsic spatial resolution (a Gaussian) is shown dashed (F_int); (2) the chromatic aberration and finite photon penetration (an exponential) is shown as the dot-dash curve (F_exp); and (3) the XMA mirror scattering (a Lorentzian) is shown dotted (F_scatt). For reference, the 4 energies at which the PANTER measurements were made are also indicated. It can be seen that the analytical forms break down above ~2 keV, when F_exp > 1 and hence F_int < 0 (see text).

Figure 2 The PANTER data and the derived analytical functions describing various components of the on-axis p.s.f. of the ROSAT XMA + PSPC combination. Top left panel: the width, 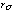, of the Gaussian describing the intrinsic spatial resolution of the PSPC (eqn 11); Bottom left: the fraction of photons, F_exp, within the exponential component due to the combined effects of chromatic aberration and the finite penetration depth of photons (eqn 13) Top right: the e-folding angle, r_scatt, of the exponential describing the shape of the component of the p.s.f. due to these effects (eqn 15); Bottom right: the fraction of photons, F_scatt, within the Lorentzian component due to scattering by the XMA (eqn 1).

(Source: Hasinger Notes, 1992 Feb 17).

Figure 3 The energy dependence of the parameters governing the shape of the 3 major components of the ROSAT PSPC on-axis p.s.f., as determined from analytical fits to Ground Calibration measurements on PSPC-A & PSPC-C in the PANTER facility. The curves are: (dashed) the width of the Gaussian 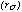component due to intrinsic spatial resolution of the PSPC; (dot-dashed) the e-folding radius 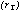of the exponential function describing the combined effects of chromatic aberration and the finite penetration of photons into the counter; and (dotted) the width of the Lorentzian r_scatt component due to scattering by the ROSAT XMA. For reference, the 4 energies at which the PANTER measurements were made are also indicated.

Figure 4 The normalizations of the 3 components of the ROSAT PSPC p.s.f. as a function of energy. The curves are the normalizations: (dashed) A_int, of the Gaussian component arising from the intrinsic spatial resolution of the PSPC (eqn 12); (dot-dashed) A_exp, of the exponential function describing the combined effects of chromatic aberration and the finite penetration of photons into the counter (eqn 16); and (dotted) A_scatt, of the Lorentzian due to scattering by the XMA (eqn 6). For reference, the 4 energies at which the PANTER measurements were made are also indicated.

Figure 5 The predicted fraction of photons, as a function of energy, scattered outside radii r_cell = 10, 100 & 600 arcsec for an on-axis source.

Figure 6a The predicted on-axis p.s.f. for the ROSAT PSPC for various energies derived from the analytical fitting of PANTER calibration data. The Gaussian, exponential and Lorentzian components are shown dashed, dot-dashed and dotted respectively, with the solid curve giving the composite. Note that in order to demonstrate the structure of the scattered component, the r-axis has been extended beyond the fov of the PSPC.

Figure 6b Close-up of inner region of the predicted (composite) ROSAT PSPC p.s.f. for various energies.

Figure 7 The predicted fraction of encircled photons for the ROSAT PSPC as a function of radius for various energies.

Figure 8 The radii encircling 50, 90 & 95% of the photons for the ROSAT XMA + PSPC, as predicted from the the analytical expressions derived from the PANTER p.s.f. calibration measurements.

Figure 9 The predicted p.s.f. (solid line) compared to the PANTER data from which it was derived.

(Source: Hasinger Notes, 1992 Feb 17).

Figure 10a The observed p.s.f. of the ROSAT PSPC in the B-band (0.1--0.188 keV) compared to that predicted from the ground calibration data. The figures are numbered as listed in Table 2. The large discrepancies, due to the effects of Ghost images in the band (see Section 1.5) are clearly apparent.

Figure 10b As for Figure 10a, but for the C-band (0.188--0.284 keV).

Figure 10c As for Figure 10a, but for the R1-band (0.284--0.5 keV).

Figure 10d As for Figure 10a, but for the R2-band (0.5--1.0 keV).

Figure 10e As for Figure 10a, but for the R3-band (1.0--2.48 keV). Note, the predicted p.s.f. for this band were calculated using the spectral data below 2.0 keV only.

---

Proceed to the next article Return to the previous article

Select another article

---

---

HEASARC Home | Observatories | Archive | Calibration | Software | Tools | Students/Teachers/Public

---

Last modified: Monday, 19-Jun-2006 11:40:52 EDT

HEASARC Staff Scientist Position - Applications are now being accepted for a Staff Scientist with significant experience and interest in the technical aspects of astrophysics research, to work in the High Energy Astrophysics Science Archive Research Center (HEASARC) at NASA Goddard Space Flight Center (GSFC) in Greenbelt, MD. Refer to the AAS Job register for full details.