NOTICE: This Legacy journal article was published in Volume 5, November 1994, and has not been updated since publication. Please use the search facility above to find regularly-updated information about this topic elsewhere on the HEASARC site.

Calibrating BBXRT

1. Overview

This article summarizes the calibration of the two solid state Si(Li) X-ray detectors and the X-ray telescopes that flew as part of Goddard Space Flight Center's Broad-Band X-Ray Telescope (BBXRT) experiment on board the space shuttle Columbia in 1990 December. BBXRT was a precursor of ASCA, and consisted of two identical telescopes with lightweight, nested, thin-foil conical imaging mirrors (Serlemitsos 1988), which focused X-rays onto two segmented spectrophotometric Si(Li) diodes located at the focal plane. During its flight, BBXRT spent roughly 185,000 secs pointing at celestial sources with typical integration times of 500 to 2,000 secs. The BBXRT observation log, containing a complete list of all scientifically useful pointings, can be found in Weaver et al. (1995). This article contains useful information for anyone wishing to analyze BBXRT data, such as discussions of the effective area and flux calibrations, flux corrections for off-axis observations, background subtraction techniques for daytime observations, and the systematic uncertainties in the effective area calibration for point sources. For details of the instrument and in-flight performance see Weaver et al. (1995) and Smale (1992).

2. The BBXRT Detectors, Mirrors, and Point Response Function

Each BBXRT detector, designated by "A" or "B", consisted of a silicon block with a grooved surface, segmenting it into 5 spatial elements or "pixels" (Fig. 1). The grooves were 0.5 mm wide and were covered with an opaque mask that also occulted 0.5 mm of the detector on either side of the groove. The radius of the central pixels (designated A0 or B0) was 5 mm giving a field of view of 3.6 arcminutes, and the total diameter including the outer pixels was 19 mm or 17.3 arcminutes. The central detector elements had about 1/4 of the background of the outer elements as well as an on-orbit energy resolution of approximately 100 eV FWHM at 0.9 keV and ~155 eV FWHM at 6 keV, while the outer pixels had a slightly poorer resolution of ~170 eV FWHM at 6 keV. The signal processing electronics gave each pixel 512 energy channels with widths of ~16 eV from channels 1 to 255 and ~32 eV from channels 256 to 511. Because of the low-energy noise threshold, the lowest usable channels in A0 and B0 are channel 16 and channel 17, respectively, which corresponds to about 0.3 keV. This ranges from channels 25 to 30 in the outer pixels, which corresponds to ~0.4 keV (Table 1).

Figure 1 illustrates the approximate orientation of the BBXRT detectors with respect to the aspect camera and projected onto the celestial sphere. The outer pixels of the A detector are labeled A1 to A4 counterclockwise on the sky. The telescope roll angle, 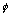increases counterclockwise and is defined such that when 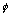= 0, the top of the camera and the top of pixel A4 point north. The B detector is rotated by 180 degrees with respect to the A detector such that A1 and B3 observe the same area of the sky. Postflight analysis indicates a slight offset between the A and B telescopes (not shown in Fig. 1). The mean displacement of B from A is 0.822 arcminutes at an azimuth of -63.24 degrees. This azimuth is measured arbitrarily from the B3/B4 boundary and represents a 63 degree rotation through B4 toward B1. Because the the A system axis was taken as the nominal pointing position of the telescope, this displacement generally leads to a lower count rate in the B detector. A correction to account for the difference in observed count rates between A and B is not included in the effective area calculations. Therefore, all fluxes are measured with respect to the A system. Here, the term "on axis" refers to a source centered in the A detector.

BBXRT used 10 cm long conical reflectors that approximated a Wolter type I mirror optical system. There were two adjacent, coaxial, and confocal arrays of cones in each mirror assembly. The mirror performance is summarized by Petre et al. (1992), and the mirror fabrication techniques and mirror parameters are described in detail by Serlemitsos (1988) and Serlemitsos et al. (1991). The point spread function (PSF) of the mirrors is broader than a single Gaussian profile. For a source observed on axis ~62% of the counts that reach the detector fall in the central pixel, ~21% fall on the mask between the pixels, and ~17% fall into the outer pixels (Smale 1992). For a source observed near the edge of a pixel or on the mask, a larger fraction of photons is lost to the mask (up to 50%). It is necessary to correct for this loss when measuring absolute fluxes (see Section 3.3). A possible energy dependence of the PSF is discussed in Section 3.4.3.

Figure 1

 Table 1: Reliability of Response Matrix at Low Energies


   Pixel  Lowest available  Energy   Lowest reliable    Energy
             pha channel    (keV)      pha channel       (keV)

     A0           16        0.29          16             0.29 
     A1           26        0.41          26             0.41 
     A2           26        0.42          26             0.42 
     A3           27        0.44          27             0.44 
     A4           25        0.41          43             0.70 
     B0           17        0.30          17             0.30   
     B1           27        0.42          39             0.60 
     B2           28        0.43          34             0.52 
     B3           28        0.45          34             0.54 
     B4           29        0.44          45             0.69
      

3. Calibration of the Detectors and Mirrors

3.1. Incomplete charge collection uncertainties

The term "incomplete charge collection" refers to charge loss mechanisms in the detector that result in an underestimation of the incident photon energy. Incomplete charge manifests itself as non-Gaussian components that occur in the response function below the main Gaussian photopeak. The shapes and magnitudes of these components vary from detector to detector (Shima et al. 1983), but they are difficult to model because their physics is poorly understood.

For simplicity, we initially modeled the incomplete charge in the BBXRT detectors as a step function (convolved with a Gaussian) starting at the energy of the incident X-ray and extending to zero energy. However, we found that (1) there was a significant incomplete-charge tail that rises toward low energies (<0.7 keV), (2) the tail was a larger effect in the calibration data than in the flight data, and (3) the tail was a larger effect in the outer B pixels than in the outer A pixels. Because the tail differs between flight and calibration data, we require fitting celestial sources to measure it. However, because of the uncertainties inherent in fitting the Crab to determine its magnitude, we have not included the tail in our response function. This lack of a correct model of the incomplete charge collection causes an uncertainty in the low-energy effective area calibration of the outer B pixels.

3.2. Data from the Crab Nebula

Observations of the Crab Nebula were made four times during the mission. Light curves of the day 3 observation in the A pixels are shown in Figure 2. The Crab Nebula was first observed for 2,300 seconds at ~3.0 arcminutes off axis, with the source flux highest in pixels A1 and B3. An attitude adjustment that began at 3.054 days mission elapsed time (MET) placed the Crab in pixels A0 and B0. This observation is designated "on axis" for calibration purposes, although the Crab was offset by about 1 arcminute toward pixel A3. The first half of the on-axis observation was performed during orbit night, while the second half was performed during orbit day.

Figure 2

The Crab Nebula X-ray spectrum can be well described by a single absorbed power law over the 1-10 keV energy band. The photon index is well known, with the average value in the literature being 2.1. There is, however, some disagreement over the observed value of the hydrogen column density along the line of sight to the Crab. The measured values for N_H are not all consistent, and the discrepancy is rather high in a few cases (see e.g., Seward 1992; Weaver 1993, Table 3.4). The mean value of the column density from the literature is N_H = (2.9 +/- 0.4) x 10²¹ cm^-2.

Complexities in the Crab's spectral and spatial characteristics have been observed at both high and low energies. The spectrum flattens at high energies due to the contribution from the pulsar. This effect is ~10% at 10 keV (Toor and Seward 1977). Below 2 keV, the angular size of the Crab increases. This is attributed to interstellar dust that causes low energy photons to be scattered into a dust halo. In fact, 11% of the total 0.5-3.5 keV flux measured with the Einstein Observatory IPC appears at a radius of greater than 1.6 arcminutes (Mauche and Gorenstein 1989). However, from a comparison of Crab spectra between pixels, we conclude that any effects of the dust-scattering halo are less than the ~15% uncertainty in the hydrogen column to the Crab, so for simplicity we did not include a dust scattering halo in our calibration model. The effective areas for the two central pixels was refined based on fitting the on-axis Crab spectrum to an absorbed power law with a photon index of 2.10 and a neutral hydrogen column density of 3 x 10²¹ cm^-2.

3.3. The Mirror Areas and Flux Corrections

To obtain the 2-10 keV assumed Crab slope, we allowed the density of vacuum-deposited gold on the mirrors to be a free parameter in the effective area calculations. The mirror areas were then generated for the entire focal plane. For simplicity, we chose to fit the Crab data from the central pixels only under the assumption the the PSF is independent of energy. However, our assumption that energy-dependent scattering by the mirrors is not important may be incorrect (Section 3.4.3).

Two vignetting corrections are currently included in the BBXRT response matrix. First, the effective area curve is normalized by 62% under the assumption that one is analyzing data from the A0 pixel for an on-axis source. This correction factor accounts for 38% of the source counts being lost, primarily to the mask and the outer pixels (Section 2), and provides accurate fluxes for sources that are more or less centered in A0. Second, for off-axis sources, energy-dependent vignetting corrections to the effective area are included in the response. These were obtained by modeling the throughput of the mirrors as a function of off-axis angle using ray-tracing techniques (Weaver et al. 1995, Fig. 10). The ray-tracing calculations have been performed for point sources only.

A third correction that has not been included in the response matrix accounts for the (often significant) loss of photons for sources observed off axis due to the presence of the masks between the detector elements. If a source happens to sit directly over a mask, up to 50% of the photons reaching the focal plane can be lost. As an illustration of the potential severity of the problem, the distribution of photons in the focal plane for a point source observed in three different locations is shown in Figure 3. Here, the azimuthal angle , is arbitrarily measured with respect to the edge of the outer pixel nearest the source position and increases toward the center of that pixel. Due to the symmetry of the outer pixels, ranges from 0 degrees to 45 degrees. Case (a) illustrates the distribution of photons for a point source that is directly on axis. For a source that is located 4 arcminutes off axis and directly over the mask (case b), the total collection efficiency is cut by one half. However, in case (c), where the source is off axis but centered in an outer pixel the total collection efficiency is higher than in case (a) due to the larger size of the outer pixels. Ray-tracing techniques have been used to calculate the fraction of counts lost to the mask for a multitude of source positions. Figure 4 provides the flux-correction factor to be used for off-axis observations for sources having off-axis angles 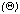ranging from 0 arcminutes to 8 arcminutes and azimuthal angles of = 0.0 degrees, 22.5 degrees, and 45 degrees.

To determine the flux for an off-axis point source, 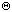and must be known. If an aspect solution is available, the R.A. and Decl. offsets and the roll angle (Weaver et al. 1995, Table 1) provide both angles. Otherwise, 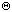and can be estimated by utilizing a ray-tracing program (currently known as KNIFE[1]) available from the HEASARC. Figure 4 gives the appropriate correction to the fluxes derived with the BBXRT response matrix. For example, for a point source having 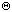= 5 arcminutes and = 45 degrees, the flux correction factor for the A detector pixel in which the source is located (the source pixel; labeled as "pixel 1" in Figs. 3 and 4) is 1.23. The flux-correction factor for each of the adjoining or "nonsource" outer pixels (labeled as "pixel 2" and "pixel 4" in Figs. 3 and 4) is ~0.02. To derive the flux of the source, divide the apparent flux derived from the spectral fit by the flux-correction factor for that pixel.

Figure 3

3.4. The Effective Area Curve

The effective area curves for the central pixels were generated by allowing the optical depths of the various sources of absorption within and above the detectors (Si, C, Al, Au) to be free parameters in fits to the Crab. Details of the procedure are given by Weaver (1993). Although the Crab was not observed in all pixels, other bright sources such as Cygnus X-1, Cygnus X-2, and Perseus were available for calibrating the outer pixels. The effective area curves for the outer pixels were calculated by fitting their spectra simultaneously with an A0 or B0 spectrum of the same source and varying the absorption parameters (and the magnitude of incomplete charge within certain limits) to give the best fit. After the absorption parameters were adjusted, the effective area curve still underpredicted the Crab data at greater than 6 keV. This high-energy tail was a 20% effect in both A0 and B0 at 10 keV, more than the 10% flattening expected due to the presence of the pulsar. The excess of photons at high energies has been corrected by multiplying the effective area by a relation of the form R = m x E + b above 05.2 keV, where m is 0.0429 and 0.055 for A and B respectively, and b is 0.772 and 0.708 for A and B, respectively.

Figure 4 a, b, and c

3.4.1. On-axis Observations

Figure 5a illustrates the best power-law fit to the on-axis A0 Crab observation, which results in 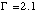and N_H = 3 x 10²¹ cm^-2. The residuals are shown in Figure 5b. Figure 6a shows the best power-law fit to the on-axis observation in B0 which also results in 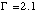and N_H = 3 x 10²¹ cm^-2. The residuals are shown in Figure 6b. Close inspection reveals that fewer counts are observed in the B detector than in the A detector below about 2-3 keV. This occurs for all B detector elements and appears to be due to the B detector being covered with a thicker gold surface contact layer than the A detector.

At the present time, the effective area is understood at the 5% level in A0 with up to 10% residuals at very low energies (<0.6 keV). The area is also understood at the 5-10% level in B0 over the 0.6 to 9 keV range. However, residuals to the Crab in B0 appear both below 0.6 keV and above 9 keV at the 10-15% level. The ~10% residuals above 9 keV appear to be due to incomplete modeling of the 8.3 keV edge caused by the nickel mesh in front of the detector. There is also a larger mismatch to the Al, Si, and Au edges in B0 than in A0, and there is a narrow feature present at 1.38 keV in B0. This feature is at worst a 10% residual, and less than 10 eV equivalent width when fit with a Gaussian. In addition, a <5% "bump" in the residuals still exists around 7.5 keV in both A and B.

The worst residuals in both detectors are at ~0.5 keV. When the on-axis Crab data are split into night and day, there is an indication that the low-energy residuals change with time, ranging from a 5% to a 15% effect. It appears that they are caused by a temporal change in the gain or low-energy resolution. The magnitude of the residuals can be measured as follows: fitting the positive ~0.5 keV feature with a narrow Gaussian (E = 0.41 keV) gives an equivalent width of less than 140 eV in A0 and less than 220 eV in B0. Fitting the negative feature gives an energy of 0.52 keV (a slightly lower energy than an oxygen edge at 0.53 keV). Fitting with a notch (width 0.03 keV) gives a covering fraction for the notch of <0.4 for A0 and <0.65 for B0.

Figure 7 shows the confidence contours for N_H versus 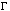derived from all pixels when the Crab is approximately on axis. The 90% confidence contours for A0 and B0 overlap, indicating that the two central pixels (the source pixels) give consistent results for the Crab. However, for the outer pixels (the nonsource pixels), the remaining systematic uncertainties 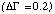are 2 to 3 times greater than the statistical uncertainties in fitting the Crab. The systematic uncertainty measured in the outer pixels may be because we have not accounted for an energy dependence in the the mirror PSF (Section 3.4.3).

3.4.2. Off-axis Observations (Source Pixel)

There are remaining uncertainties for outer pixel data. Although most of the outer A pixels are reliable down to their lowest usable energies (Table 1), the A4 pixel is particularly noisy and so is only reliable down to about 0.7 keV. Also, because of the uncertainty in modeling the incomplete charge collection, the outer B pixels are reliable only to 0.5-0.7 keV.

The confidence contours for N_H versus 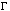for all pixels when the Crab is 3.0 arcminutes off axis are shown in Figure 8. In this case, the source pixels are A1 and B3. The index measured for A1 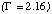is steep and is inconsistent with the index measured for B3 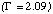. This represents the largest discrepancy still remaining between pairs of source pixels 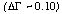, although this should be an observable problem only for bright sources (greater than or equal to ~10 counts sec^-1) with good statistics. The remaining discrepancy between A1 and B3 is smaller than the general systematic uncertainties observed between outer, nonsource pixels when the Crab is on axis (Fig. 7).

3.4.3. On- and Off-Axis Observations (Nonsource Pixels)

For a point source observed with BBXRT, there are still large systematic residuals when attempting to use data that are not from the source pixel. During the on-axis observation, the Crab was actually offset by about 1 arcminute toward A3 and B1 (Section 3). From Figure 9, it can be seen that for this observation, for 5 out of 6 of the pixels other than A0, B0, A3, and B1 (i.e., those pixels in which the majority of the Crab flux is coming from a region greater than 5 arcminutes away from the core of the PSF), the spectra tend to be flatter. The effect is even more obvious during the off-axis Crab observation (Fig. 8). In this case, the source pixels are A1/B3 and A0/B0, while A3/B1 are the furthest from the source in detector coordinates. Clearly, the measured photon indices become much flatter with increasing angular distance from the Crab.

The flattening in the Crab spectrum observed in nonsource pixels is due to the increased presence of a high-energy tail in data obtained from a greater than 5 to 6 arcminute radius away from the center of the source in detector coordinates. This flattening can be seen in power-law fits to data from the outer pixels when the Crab is observed approximately on axis. Figure 9 shows a plot of the ratio of the A2 and B4 Crab spectra to an absorbed power law model having an index of 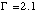. In this case, the best-fit N_H is the "expected" value of 3.0 x 10²¹ cm^-2. A tail at high energies (which is a 20% effect) is observed in the ratio of the data to the model.

Figures 5a and b

Figures 6a and b

Figure 7

Figure 8

Figure 9

One explanation for the high energy tail seen in the nonsource pixels is an energy dependence of the mirror point response function for large radii. Measurements appropriate to test for an energy dependence are not available for the BBXRT mirrors. However, this effect has been observed for the ASCA mirrors (H. Kunieda and the ASCA calibration team, 1993 private communication). Preliminary measurements of the ASCA mirrors indicate that 7% of the flux at 2 keV, 15% of the flux at 5 keV, and 17% of the flux at 8 keV is scattered from the core of the mirror PSF into a greater than 6 arcminute radius (thus extending the wings of the PSF for higher energies). This energy-dependent scattering has the right magnitude to explain the high-energy tail observed in the outer-pixel BBXRT data when the Crab is centered (Fig. 9), although off-axis measurements of the Crab indicate that this tail is an even larger effect than expected for a simple energy dependence of the PSF.

Recall that we used only the A0 data (essentially from the beam core) to modify the effective area to fit the Crab (Section 3.3). However, if scattering out of the beam core is energy dependent, then a larger fraction of high-energy photons than low-energy photons are scattered out of the core. This means that the measured slope of the Crab when using only central pixel data should be "too steep". We may have inadvertently corrected for this steepening by altering the mirror gold density by ~5%. Therefore, it is likely that our calibration contains a systematic error in the sense that measured spectral slopes will be too flat by about 5 to 10% in 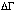when using data from a source pixel, whether the source is observed on or off axis. However, this small effect should only be noticeable for sources having count rates greater than ~10 counts sec^-1. For data from a nonsource pixel, the systematic flattening at high energies can easily dominate statistical uncertainties for most point sources (Figs. 8 and 9).

4. Flux Calibration

To determine the normalization of the BBXRT effective area curve using the Crab Nebula, corrections must be applied to the observed count rate because some X-ray events are not recorded in the telemetry. The effects of dead time (see Smale 1992), flagging, and pulse pile-up were examined using all of the events in the telemetry for a one second interval for the on-axis A0 Crab observation at 3.056 days. After correcting the observed count rate for these effects, we find R_{obs}(spectrum) = 0.648 R_{true}. An absorbed power-law fit to the on-axis Crab observation in A0 gives a normalization of 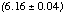photons sec^-1 keV^-1 cm^-2 at 1 keV (90% confidence errors). After applying the above correction, this results in

N(E) = 9.51 E^-2.11 e^((E)N_H)

where N(E) is given in photons sec^-1 keV^-1 cm^-2. Our derived normalization at 1 keV agrees well with the normalizations measured by previous experiments (Toor and Seward 1974; Burrows 1982; Turner et al. 1989), and indicates that our Crab flux is accurate to within ~15%.

This flux calibration applies only to sources observed on axis in the A detector. To account for the mask for off-axis observations, one must apply a flux correction factor (Section 3.3).

5. The Detector Background

There are four major contributions to the BBXRT detector background: internal background, particles, events from the diffuse X-ray background (DXRB), and X-ray contamination at low energies from solar radiation scattered off Earth's atmosphere. This "Earthglow" is the dominant low energy component for daytime observations, and its intensity correlates with the "Earth angle", defined as the angle between the telescope pointing direction and the direction of the center of the Earth. During nighttime observations, the instrumental background and the DXRB contribute equally at low energies. See Weaver et al. (1995) and Smale (1992) for a discussion of background rejection techniques.

5.1. The Non-X-Ray background

The non-X-ray detector background is made up of electronic noise, microphonics, and particle events. Electronic noise is forced to be a small effect by setting the discriminator thresholds above ~0.3-0.5 keV. Microphonics are different from noise associated with the ordinary detector leakage current, and bursts of microphonics events which typically last about 2 milliseconds can be eliminated during data extraction for weak sources (Smale 1992).

Particle events are the primary source of the non-X-ray background. The outer-pixel count rates for the non-X-ray background (from times when BBXRT was not passing through the South Atlantic Anomaly [SAA]) are plotted against the detector guard rate[2] in Figure 10. A correlation between count rate a guard rate is clearly present, and it is approximately linear for guard rates greater than about 1000 and less than about 2000. This correlation allows the non-X-ray component of the background to be easily predicted for a known guard rate. Below a guard rate of 1000, the non-X-ray background reaches a lower threshold at about 0.15 and 0.18 counts sec^-1 in the summed outer A pixels and B pixels, respectively. The magnitude of the non-X-ray background (excluding microphonics) is 1.5 x 10^-3 counts keV^-1 sec^-1 in each central pixel and ~8 x 10^-3 counts keV^-1 sec^-1 in each outer pixel, with the exception of A4 which has a very strong non-X-ray background component below 0.7 keV.

Figure 10

5.2. The Diffuse X-Ray Background during Orbit Night

For nighttime source observations and Earth angles greater than 90 degrees, the external X-ray background is due solely to the DXRB. For a guard rate of ~1000, the count rate in the DXRB is approximately equal to the non-X-ray background count rate over 0.4-0.6 keV, and can be one half the non-X-ray background count rate over 0.6-1.0 keV. However, the DXRB flux is less than 10% of the non-X-ray background at energies greater than 2 keV. The diffuse background count rate remains roughly the same for all observations because BBXRT is not particularly sensitive to spatial fluctuations in the DXRB due to short integration times.

5.3. The Atmosphere and the X-Ray-Bright Earth

The shuttle's orbit places it in Earth's upper atmosphere at an altitude of ~200 km. At this altitude, BBXRT suffers from a large amount of low energy (0.3-1.0 keV) contamination during "day-side" observations. This contribution to the X-ray background occurs when X-ray photons from the solar corona are scattered by Earth's upper atmosphere. The relevant processes involved are Thomson scattering and fluorescent scattering. BBXRT encountered two states of bright Earth emission: an "active" state when the Sun was flaring and a "quiet" state when the Sun was more or less quiescent. During the active state, when the Sun emits higher energy photons, emission lines of Mg, Si, and Ar are observed as well as a strong thermal continuum and Fe L emission. Fortunately, no flares occurred during daytime source observations. During the quiet state, we see a weaker thermal continuum and scattered Fe L emission as well as O and N_2 fluorescence lines.

Figure 11 illustrates how the <2 keV bright Earth count rate changes with Earth angle. The channel range 27-42 emphasizes the oxygen line, which is brightest at Earth's limb (between 70-80 degrees). There is a large drop in the count rate above 80 degrees although oxygen contamination persists up to 150 degrees. Channels 45-80 emphasize the change in the Fe L count rate with distance from Earth's limb. There is once again a rapid drop above 80 degrees, although there are significant counts in the Fe L complex even at 100 degrees. For higher energies (channels 80-120), there is essentially no contribution to the background for Earth angles larger than 80 degrees.

Figure 11

6. Background Subtraction

The non-X-ray component of the BBXRT background can be easily predicted as follows. First, the average guard rate during the source observation (the "source guard rate" or SGR) is determined (see Weaver et al. 1995, Table 1, for a listing of guard rates). Second, the count rate of the non-X-ray background (which has a mean guard rate, MGR, of 1259) is altered by a "background scale factor", BSF = MGR/SGR, to match the count rate that is predicted from the linear relation in Figure 10. Finally, the scaled background is subtracted from the source data. The non-X-ray background reaches a lower threshold at a guard rate of 1000 and should not be scaled below this value. The background subtraction procedure discussed here only applies to observations out of the SAA with an average accumulated guard rate of less than or equal to ~1400.

Creating an appropriate background for an observation obtained during orbit night consists of adding together (1) a DXRB spectrum which has its non-X-ray background already subtracted and (2) the non-X-ray detector background scaled as described above. An appropriate background spectrum for a daytime observation consists of (1) the daytime background (which contains scattered light plus the DXRB) accumulated for the average Earth angle of the source observation, minus its non-X-ray background, plus (2) the non-X-ray detector background that has been scaled as described above.

The adopted background subtraction algorithm is given below. Here, BG_N is the nighttime (diffuse only) background, BG_I is the non-X-ray background, BG_D(EA) is the daytime (diffuse plus scattered) background as a function of Earth angle, NGR (= 1274) and DGR (see Table 2) are the average guard rates of the nighttime and daytime backgrounds, respectively, and SGR is the average guard rate during the source observation. Night background, non-X-ray background, and daytime background files for various Earth angles have already been extracted and are available through the HEASARC for those wishing to use the following algorithm to construct backgrounds appropriate for their observations.

BBXRT background subtraction algorithm:

ORBIT NIGHT:

Data - BG_N - BG_I (scaled using MGR/NGR)] - BG_I (scaled using MGR/SGR);

ORBIT DAY:

Data - BG_D(EA) - BG_I(scaled using MGR/DGR)] - BG_N(scaled using MGR/SGR).

Because BBXRT has five detector elements, the estimation of background is fairly straightforward for weak point sources observed on axis. In this case, the simultaneous outer-pixel data provide a direct estimate of the background during the observation.

Table 2: Parameters for Daytime Backgrounds: BG_D(EA)

  Earth Angle range    	 DGR       BSF 
     (degrees)

   	30-50      	 1066      1.18 
   	50-70       	 1060      1.19 
   	70-80       	 1033      1.22
   	80-90       	 1229      1.02 
   	90-100      	 1126      1.12 
       100-110      	 1228      1.03 
       110-120      	 1210      1.04 
       120-130      	 1209      1.04 
       130-150      	 1225      1.03 
       150-180      	 1010      1.25
 

7. Remaining Systematic Uncertainties

We currently understand the BBXRT effective area curve at the 5-10% level between 0.7-10 keV and at the 10-15% level below 0.7 keV for data from a source pixel for both on- and off-axis observations of point sources. Further refinements of the effective area await postflight ground calibration measurements. A summary of the remaining calibration uncertainties are listed below.

(1) Our step-function incomplete charge model does not properly account for the low energy (<0.7 keV) shape of the incomplete charge distribution. This mainly affects the B detector, and causes data from less than 0.6-0.7 keV in pixels B1, B2, B3, and B4 to be unusable.

(2) A high-energy excess still exists in the B0 pixel above 9 keV (a ~10% effect). This is probably due to incorrect modeling of the Ni edge at 8.3 keV.

(3) Low-energy residuals in the Crab data are seen. These may vary with time and are a 5-15% effect below 0.6 keV.

(4) Residuals still remain around the Al, Si, and Au edges due to a mismatch of our model to the Crab data (a 5% effect).

(5) Because we have not accounted for any energy-dependent scattering by the mirrors, there is likely a systematic error for on-axis sources that causes the 2-10 keV slopes in A0 and B0 to be too flat by about 5-10%. This should only be significant for bright targets.

(6) The systematic error in the measurement of the Crab slope between pairs of outer pixels (for source pixels) is +/-0.10 in photon index.

(7) The measured power-law indices for Crab spectra from non-source pixels are too flat by 10-25%. This is a greater than or equal to a ~10-20% effect in flux at >5 keV, and may result from not accounting for an energy-dependence in the mirror PSF.

References:

Burrows, D. 1982, Ph.D. Thesis, University of Wisconsin

Mauche, C.W. and Gorenstein, P. 1989, ApJ, 336, 843

Petre, R., Serlemitsos, P.J., Marshall, F.E., Jahoda, K. and Kunieda, H., 1992, Proc. S.P.I.E., 1546, 72

Serlemitsos, P. J. 1988, Appl. Opt., 27, 1447

Serlemitsos, P.J., Marshall, F.E., Petre, R., Jahoda, K., Boldt, E.A., Holt, S.S., Mushotzky, R., Swank, J., Szymkowiak, A., Kelley, R., and Loewenstein, M. 1991, in Frontiers of X-ray Astronomy, eds. Y. Tanaka and K. Koyama (Tokyo: Universal Academy Press), p 221

Seward F. 1992, Legacy, 2, p. 47

Shima, K., Nagai, S., Mikumo, T. and Yasumi, S. 1983, Nuclear Instruments and Methods in Physics Research, 217, 515

Smale A. P. 1992, Legacy, 2, p. 17

Toor, A. and Seward, F.D. 1974, AJ, 74, 995

Toor, A. and Seward, F.D. 1977, ApJ, 216, 560

Turner, M. J. L., et al. 1989, in Proc. 23rd ESLAB Symp. on Two Topics in X-Ray Astronomy, eds. J. Hunt and B. Battrick, ESA SP-296, Vol 2, 769

Weaver, K. A., et al. 1995, ApJSuppl, in press

Weaver, K. A. 1993, Ph.D. Thesis, University of Maryland

Proceed to the next article

Return to the previous article

Select another article