ME DEAD TIME CONSIDERATIONSFollowing a general survey of the EXOSAT instrumentation timing and dead time characteristics (Express No. 5, p.31) a number of discussions have taken place at the Data Analysis Workshop and elsewhere to try to resolve an outstanding discrepancy in the ME dead time correction factor and its functional form. All observatory software and analysis routines use an empirical effective sample rate to correct spectral counts to fluxes through the known dead times of the HK QEP counts. Although this method produces the 'correct' result, several users, notably C. Page at Leicester and A. Tennent at Cambridge, have pointed out that for certain high time-resolution measurements precise knowledge of the factors contributing to the total loss is important. This note explores in more detail the predicted loss of events from sampling, inherent electronic dead times and subsidiary effects, which taken together give good agreement with the observational data.Figure 1 shows the distribution of time tags (raw channel counts) of a sample of ME events (245760 - mainly background), selected on board according to valid E (= QEP) with a sample scheme of E, TT at 4K s-1 (sampling scheme eg. E, ID or E, ID, TT has no effect). Note that the maximum time tag possible is 31, determined by sample interval/clock interval (244.1 µs/7.63 µs) and that the following contributions to overall dead time are evident.
Simple Poisson statistics give the dead time correction factor associated with (a). fa = MT (1 - exp[-MT])-1 where fa = correction factor M = true total qualified event rate T = sample period. M can be obtained with sufficient accuracy from the HK QEP counts, corrected for the electronic chain coincidence logic dead time for events > Emin (factor ~ 1.005).
A fixed correction (~0.25 X TM clock period) must be added to
account for the deficit in channel 0, representing the time between the sample
pulse trailing edge and the reset (~2 X 1 MHz clock pulses - ref. figure 2). For
a Hz sample rate, 1.91 µs/244.1 µs gives approximately 0.8%, in fair agreement with the loss of 2200 events in an
expected 269.000. An analysis of figure 2 with respect to the assignment of chs.26, 27-30 time tags to channel 31, shows that these events must be at a time such that the reset pulse (after last sample pulse) occurs while the ADC conversion (33 µs) is in progress, that is within the period-defined by X-ray events X1 and X2 (TT/QEP at t1 and t2). In these cases, the event is processed by the next sample cycle and is assigned a time tag of 31 (maximum). Because the current sample pulse does not process this data there is an effective extra dead time for these events only (fraction occurring in channels 26, 27-30) of 1 sample cycle. Thus the overall loss of data from this effect can be determined as the probability of the events occurring in channels 26, 27-30 having a second event within the time period of the next sample cycle. Again from Poisson statistics, the dead time correction factor which accounts for (a), (b) and (c) can be determined as: fTOT = MT{ 1-exp[-MT'] - exp[-M(T'-t)] (1-exp[-Mt])(1-exp[-MT'])} (2) where fTOT = total correction factor t = ADC conversion time (33 µs) T' = T-TR, TR = 1.91 µs = 'sampling/reset' dead time Table 1 shows the correction factor obtained from equations (1) (for sampling rates of 4096 Hz and 3569 Hz) and (2) for various housekeeping event rates. Note that the concept of an effective sampling rate is not totally invalid given the 'loss' of a sample cycle for the events of type (c) and in most - cases equation (1) with an effective sample rate of 3569 Hz and the true count rate determined from the housekeeping count rate is a sufficiently precise approximation to the total dead time correction. The best results are however obtained by using equation (2) as shown in table 2 which gives a comparison of the observed and predicted count rates of selected sources.
D. Andrews 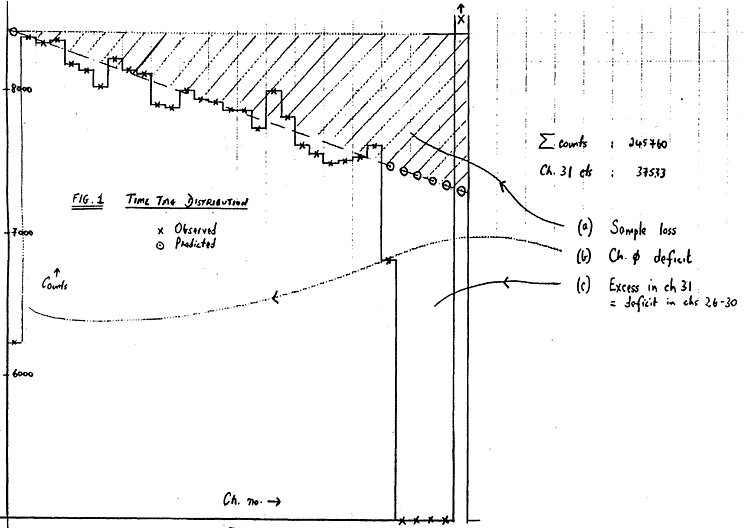 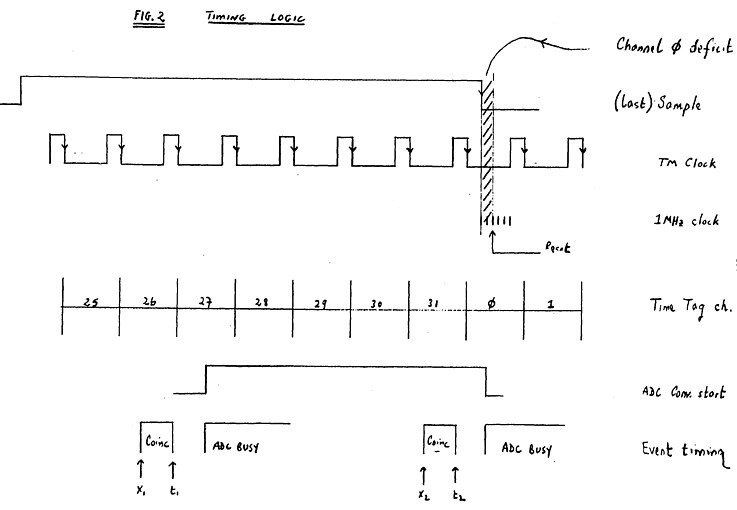 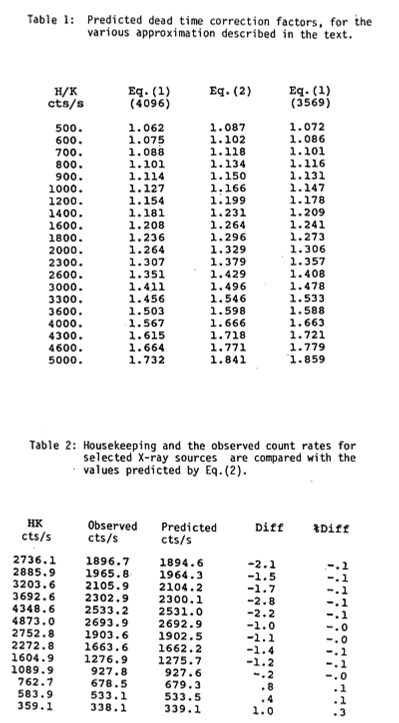 Page authors: Lorella Angelini Jesse Allen HEASARC Home | Observatories | Archive | Calibration | Software | Tools | Students/Teachers/Public Last modified: Thursday, 26-Jun-2003 13:48:32 EDT HEASARC Staff Scientist Position - Applications are now being accepted for a Staff Scientist with significant experience and interest in the technical aspects of astrophysics research, to work in the High Energy Astrophysics Science Archive Research Center (HEASARC) at NASA Goddard Space Flight Center (GSFC) in Greenbelt, MD. Refer to the AAS Job register for full details. |
HEASARC Staff Scientist Position - Applications are now being accepted for a Staff Scientist with significant experience and interest in the technical aspects of astrophysics research, to work in the High Energy Astrophysics Science Archive Research Center (HEASARC) at NASA Goddard Space Flight Center (GSFC) in Greenbelt, MD. Refer to the AAS Job register for full details.
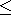1 event per sample interval (shaded area).