|
|
BBXRT
 Text from
Legacy 2
Text from
Legacy 2
The Broad Band X-ray Telescope (BBXRT) was flown on the space shuttle
Columbia (STS-35) on 1990 December 2-December 11, as part of the
ASTRO-1 payload. The flight of BBXRT marked the first opportunity for
performing X-ray observations over a broad energy range (0.3-12 keV)
with a moderate energy resolution (typically 90 eV and 150 eV at 1 and
6 keV, respectively). This energy resolution, coupled with an extremely
low detector background, made BBXRT a very powerful tool for the study
of continuum and line emission from cosmic sources. The observing
program was designed to be an even mix of Galactic and extragalactic
targets, although the Galactic Center region was not available due to
the time of year that BBXRT was launched.
BBXRT was designed and built at the Laboratory for High Energy Astrophysics
at NASA/GSFC, with Dr. Peter Serlemitsos as Principal Investigator. During
the mission, the instrument was controlled by the scientists and staff of
the
X-ray group from an operations center at GSFC, and the group as a whole
handled mission planning and real-time data analysis.
BBXRT was in orbit for almost exactly nine days. The instrument was powered
up three hours after launch and remained so until approximately six hours
before reentry. The detector system was powered up for nearly the entire
time, collecting source, background or calibration data. The instrument
behaved nearly flawlessly on orbit. The sole source of difficulty was due
to occasional hang-ups during the first few days of the processing
electronics associated with the CID aspect camera. These were eventually
eliminated by modifying the settings of a few on-board processing
parameters. The cryostat temperature remained stable within approximately
two degrees over the course of the mission, and the instrument alignment
was unchanged. All other housekeeping parameters were monitored during the
mission and examined post-flight. There were no variations outside nominal
values.
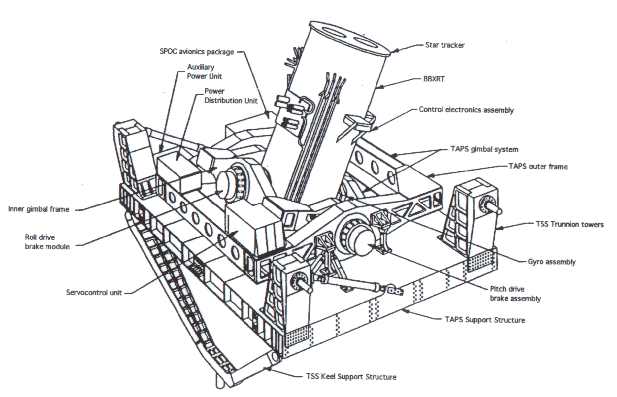
Diagram of the BBXRT support structure
Unfortunately, there were other problems which affected the total mission
efficiency. In particular, both the IPS, on which the UV instruments were
mounted, and the Two-Axis Pointing System (TAPS) experienced difficulties.
The primary consequence to BBXRT of the IPS difficulties was that the
entire pre-planned, optimized mission time-line was dropped and the
mission was replanned on a day- by-day basis with lower efficiency (more
time spent in Earthblock, for example). The TAPS problems reduced BBXRT's
observing efficiency even further. No stable pointings were accomplished
for the first 60 hours of the mission because of an improperly compensated
gyro drift rate. Once the gyro drift was removed, the TAPS was found to be
capable of pointing quite stably, with a drift rate of less than 0.1
arcsecond/second. It was then discovered that the accuracy to which TAPS
could acquire a source was typically 2-5 arcmin, resulting in a several
real-time tweaks of the pointing direction. Moreover, the pointer
experienced glitches during maneuvers between sources, inducing on each
occasion a several-arcmin systematic error on the pointing accuracy, and
requiring each time the use of an orbit night to realign the gyros by
pointing the star tracker at bright stars. Finally, a day before reentry,
an instability in the TAPS pointer made it exceed its hardware travel
limits, whereupon it became permanently engaged in its backup landing
lock. This forced BBXRT to spend the last three orbits of observations
using the Orbiter jet-firings themselves as the only source of pointing.
(The sources affected are Puppis AB and M87, both observed after MET day
8.38.)
In spite of these problems, BBXRT achieved a total of 185,000 seconds of
observation time on cosmic X-ray sources. An additional 100,000 seconds of
the total available observing time will be usable for studies of the
diffuse X-ray background. A total of 157 observations of 82 X-ray sources
was achieved, with typical observation times ranging from 300 to 3000
seconds (note that a single pointing with a tweak in the middle is counted
as two 'observations').
BBXRT (Serlemitsos et al 1984, 1992) consists of two co-aligned
telescopes with focal length 3.8m and diameter 40cm. Each telescope
contains a thin-foil conical mirror assembly consisting of 118
curved, gold-plated aluminum reflectors, and a segmented,
cryogenically-cooled lithium-drifted silicon spectrometer at the focal
plane. The optical system as a whole provides a total collecting area
of 765 cm2 at 1.5 keV, and 300 cm2 at 7 keV.
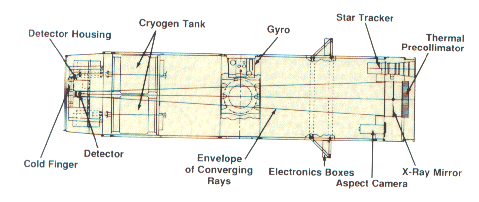
Diagram of the BBXRT telescope
Each of the detectors, 'A' and 'B', is subdivided into five pixels,
each with 512 energy channels. The central pixels (A0, B0) have a
field of view 4 arcmin in diameter, and the outer pixels
(A1-A4, B1-B4) extend the total field of view to a diameter of 17.4
arcmin. The energy channel width is 16 eV for channels 0-255 and
32 eV for channels 256-512. The B detectors are rotated by 180
degrees relative to the A detectors such that e.g., A1 and B3
co-observe the same area on the sky. Five data quality bits
accompany each detected event. Between the pixels is a mask 1.5
arcminutes across.
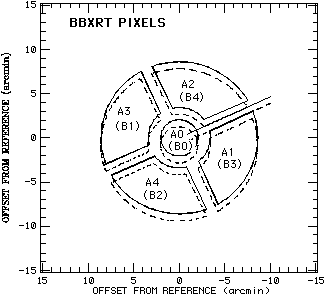
Relative orientation of the BBXRT pixels
The optical plate holding the mirrors also contains a CID camera
for real-time aspect determination and a star tracker for updating
the pointing system gyro reference. The instrument structure for
BBXRT is 4.1m long and 1m in diameter, and weighs 840 kg. During
the mission it was attached to its own dedicated pointer in the
shuttle bay, the Two-Axis Pointing System (TAPS), a generic,
two-axis gimbaled pointer supplied by GSFC which was capable, in
principle, of achieving stable pointing to arc minute accuracy.
The other three telescopes making up the ASTRO-1 payload utilized
a separate pointer.
[BBXRT Home]
[About BBXRT]
[Archive]
[Software]
[Gallery]
[Publications]
Page authors: Lorella Angelini Jesse Allen
HEASARC Home |
Observatories |
Archive |
Calibration |
Software |
Tools |
Students/Teachers/Public
Last modified: Monday, 20-Apr-2020 15:20:38 EDT
|
 Text from
Legacy 2
Text from
Legacy 2



