NOTICE:This Legacy journal article was published in Volume 2, November 1992, and has not been updated since publication. Please use the search facility above to find regularly-updated information about this topic elsewhere on the HEASARC site. |
A Recalibration of the EXOSAT
Diffraction Gratings
and Steven M. Kahn
Department of Physics
University of California, Berkeley
Abstract
A set of exceptionally high-quality spectra of Sco X-1 obtained with the Transmission Grating Spectrometers on EXOSAT motivated the need for a detailed model for the efficiency of the diffraction gratings on these instruments. We have developed a physical model for the diffraction efficiency, based on pre-flight calibration data. The model, without adjustments, quantitatively accounts for the large count rates seen at large dispersion angles in the Sco X-1 images. We describe this recalibration, and indicate to what extent analysis of archival data may be affected by the new efficiencies.
1 Introduction
A first examination of the spectral images obtained on Sco X-1 with the two Transmission Grating Spectrometers on EXOSAT revealed a systematic excess of observed counts over predicted counts at large apparent wavelengths, for any reasonable model for the incident spectrum (any reasonable continuum model with non-zero interstellar absorption). The excess was highly significant, growing to more than an order of magnitude at the longest wavelengths.
It appeared unlikely that these photons represent real first-order EUV radiation, given the strong interstellar absorption at the longer wavelengths. For example, after allowing for a reasonable fit to the short-wavelength continuum, and assuming a reasonable interstellar column density of NH ~ 1021 cm-2 the excess can be described with a very soft blackbody (TBB ~30 eV). However, the implied luminosity is an unreasonably large LBB ~ few times 1037 erg sec-1! We therefore assumed that the excess was caused by some systematic effect in the instrument or reduction procedure. The reason this effect had not been seen before in any other source had to be attributed to the extreme brightness of Sco X-1, revealing low-intensity features that normally remain hidden in noise or background.
The excess could not be attributed to imperfect background subtraction: dispersed photons are clearly visible almost all the way out to the edge of the detector, corresponding to a first order wavelength of ~200 Å (400 Å) for the 1000 (500) lines mm-1 grating (for a general description of the EXOSAT Low Energy Imaging Telescopes and Transmission Grating Spectrometers, see de Korte et al., 1981; Brinkman et al., 1980; Paerels et al., 1990).
Uncalibrated variations in the instrument efficiencies due to systematic effects in the CMA quantum efficiency, the filter transmission, or the mirror reflectivity could be excluded, as they would have been noticed before. Similarly, an uncalibrated 'bump' in the grating diffraction efficiencies would have stood out in the spectra of softer sources with a known spectrum, (e.g., the isolated hot white dwarfs). The most likely explanation for the apparent excess is that it is due to the cumulative effect of short-wavelength (5-20 Å) photons, dispersed into high spectral orders (m = 6 and beyond). These are presently not included in the efficiency model for the grating; the calibration database has data up to spectral order m = 5. This implied that a revision and extension of the grating efficiencies was necessary. Of course, the very highest order dispersed photons hardly yield significant additional constraints on spectral models for Sco X-1. However, the shortest wavelength at which an excess was seen (depending on the model for the incident spectrum) was close enough to the K edge of neutral oxygen that we felt that a more robust model for the instrument efficiency was needed in order to perform an unambiguous measurement of the depth of this edge in the spectrum of Sco X-1.
2 Grating Efficiency Calibration Data
The grating efficiency, defined as the ratio of the flux into a given spectral order at a given wavelength, to the flux incident on the detector without the grating in the beam, was calibrated for both the 1000 and the 500 lines mm-1 gratings in a series of X-ray exposures on the integrated instrument package (mirror plus grating plus filter plus detector) in the long beam test facility of the Max Planck Institut fur Extraterrestrische Physik at Garching, Germany. Data were taken at a number of characteristic X-ray wavelengths, the best sets being those at Si K, Al K, Cu L, F K, O K, C K, and B K. The grating efficiencies were derived using an explicit model for the mirror reflectivity, filter transmission, and detector quantum efficiency, as a function of wavelength. Data up to and including spectral order m = 5 were compared with simple models for the grating efficiency as a function of wavelength. For instance, at long wavelengths, the gold grating bars are completely opaque to X-rays, and the grating efficiency is a unique function of the slit-to-period ratio, a/d, and spectral order m. At shorter wavelengths, there is interference of phase-shifted radiation passing through the bars of the grating, with radiation passing through the slits, causing the efficiency curve to exhibit a maximum in wavelength; the location and shape of this maximum are a strong function of grating bar thickness, cross-sectional shape, and spectral order.
It was found that the simplest models for the efficiency, based on a grating model for rectangular bar cross-section, and characterized by a unique bar thickness, b, and slit-to-period ratio a/d, did not satisfactorily fit the measured efficiencies. Since the measured efficiencies were estimated to be accurate to better than 10%, a simple spline fit to the measured efficiencies was taken to be a sufficient model for interpolation between the calibration wavelengths. Of course, in order to extrapolate in spectral order, we do need a physical model for the grating efficiency.
The shortest wavelength calibration images actually show significant flux up to order m = 10 (at the longer wavelengths, the highest orders are off the detector), and we reanalyzed these data in order to build a model for the efficiency extending out to high order. Figure 1 shows an example of such a calibration spectrum (zero order has been subtracted), taken at 8.34 Å (Al K). Radiation is detected up to order m = 10.
Figure 1 EXOSAT 1000 lines mm-1 Transmission Grating Spectrometer calibration spectrum at Al K (8.34 Å); zero order and background have been subtracted. Diffraction up to 10th order can be seen.
3 A New Model for the EXOSAT Grating Efficiencies
The calibration dataset we used consisted of the efficiencies measured previously, up to order m = 5. We reanalyzed two calibration images, at Al K (8.34 Å) and Cu L (13.34 Å), extracting efficiencies for orders m = 6 - 10. We first concentrated on the 1000 lines mm-1 grating, because data taken with this grating will be the most valuable in the case of Sco X-1 on account of their higher spectral resolution.
The zero-order and background subtracted one-dimensional spectrum was fitted with a model consisting of a set of discrete emission lines of variable amplitude at the positions predicted from the known dispersion relation for the grating. A simple power law, of the form  was added, to account for residual zero-order contamination and continuum bremsstrahlung from the electron impact X-ray source. This model spectrum was convolved with the spectrometer response function, which at these short wavelengths is simply equal to the telescope point-source response. At the largest dispersion angles, some degradation of the response due to optical aberrations should set in; however, in the present case the degradation remains small and does not critically affect our results. Left- and right-order amplitudes were averaged after they had been found to be consistent to within the errors. We devided the amplitudes in order m by the amplitude in first order to obtain the efficiency ratios
was added, to account for residual zero-order contamination and continuum bremsstrahlung from the electron impact X-ray source. This model spectrum was convolved with the spectrometer response function, which at these short wavelengths is simply equal to the telescope point-source response. At the largest dispersion angles, some degradation of the response due to optical aberrations should set in; however, in the present case the degradation remains small and does not critically affect our results. Left- and right-order amplitudes were averaged after they had been found to be consistent to within the errors. We devided the amplitudes in order m by the amplitude in first order to obtain the efficiency ratios 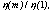 to divide out the efficiencies of the other instrument components. The resulting data were compared with an explicit model for the grating efficiency.
to divide out the efficiencies of the other instrument components. The resulting data were compared with an explicit model for the grating efficiency.
We calculated the diffraction efficiency by numerically summing the complex amplitudes of elementary waves along one grating period. The attenuation and phase shifts incurred by radiation passing through the gold grating bars was calculated using the optical constants compiled by Henke et al. (Henke et al., 1981). The grating bars were assumed to have ellipsoidal cross section, as suggested by microscope pictures of the actual grating. This grating model has two free parameters: the slit-to-period ratio, a/d, and the semiminor axis, b,of the ellipsoidal cross-sectional shape.
In principle, one can fix these parameters separately. In the long wavelength limit, the grating bars become opaque and the diffraction efficiency is a unique function of a/d and spectral order,
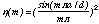
and a single set of efficiencies is sufficient to determine a/d. For a/d = 1/2, the design goal, dispersion into the even orders vanishes. Comparison with the calibration data shows that a/d is indeed close to 1/2, but no single value of a/d adequately describes all orders simultaneously. The even orders are very sensitive to small deviations from a/d = 1/2. Consequently, we assumed a distribution of a/d-values to exist over the grating, peaked near a/d = 1/2. For convenience, we assumed the shape of the distribution to be Gaussian. The efficiency of the grating was calculated by integrating the single-a/d efficiencies over the distribution. The mean, (a/d)0, and width,  (a/d), of the distribution were determined from a
(a/d), of the distribution were determined from a  -fit to all calibration data. A well-defined minimum in
-fit to all calibration data. A well-defined minimum in 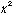 exists at (a/d)0 = 0.46 and
exists at (a/d)0 = 0.46 and 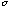 (a/d) = 0.04.
(a/d) = 0.04.
Similarly, we assumed a Gaussian distribution of grating bar thicknesses, b. The mean, b0, and width, 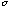 (b), were determined with (a/d)0 and
(b), were determined with (a/d)0 and 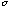 (a/d) held fixed at the above values. A well-defined minimum exists at b0 = 2.9 x 10-5 cm and
(a/d) held fixed at the above values. A well-defined minimum exists at b0 = 2.9 x 10-5 cm and 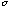 (b) = 2.0 x 10-5 cm.
(b) = 2.0 x 10-5 cm.
The efficiencies calculated from this model agree reasonably well with the calibration data. Figure 2 shows a comparison of model curves for 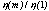 together with calibration data. Some discrepancies are evident, most prominently in the high orders, and in second order at the shortest calibration wavelength (Si K). These discrepancies indicate that additional effects not included in the grating model affect the efficiency, such as perhaps non-Gaussian distribution of the grating parameters, deviations from ellipsoidal bar shapes, and uncertainties in the optical constants of gold.
together with calibration data. Some discrepancies are evident, most prominently in the high orders, and in second order at the shortest calibration wavelength (Si K). These discrepancies indicate that additional effects not included in the grating model affect the efficiency, such as perhaps non-Gaussian distribution of the grating parameters, deviations from ellipsoidal bar shapes, and uncertainties in the optical constants of gold.
The higher-order discrepancies are less significant, since the experimental errors become larger, and are progressively more subject to systematics. The Si K data at 7.04 Å are close to the M absorption edge complex of gold (3.62-5.62 Å). Close to the edges, the optical constants are the most uncertain, so that the discrepancies between the efficiency model and the calibration data is not too surprising. We therefore decided to compose our final grating model of a spline fit to the experimentally determined efficiencies in orders 0-5 (as before), and to adopt the grating model to extrapolate to orders 6 and beyond.
Figure 2 Ratios of diffraction efficiencies relative to first order, for the 1000 lines mm-1 grating. Black squares are the measured ratios, solid lines are calculated from the final model for the grating efficiency, with (a/d)0 = 0.46, 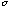 (a/d) = 0.04; b0 = 2.9 x 10-5 cm,
(a/d) = 0.04; b0 = 2.9 x 10-5 cm, 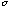 (b) = 2.0 x 10-5 cm. The numbers indicate the various diffraction orders.
(b) = 2.0 x 10-5 cm. The numbers indicate the various diffraction orders.
4 Comparison with Sco X-1
With the model efficiencies calculated as described above, we can now verify that dispersion of short wavelength photons into a large number of high spectral orders actually dominates the count rates at large dispersion angles in the Sco X-1 images. We fitted a simple, rough continuum model to a spectrum obtained in 1 hr of exposure on 1983/220 with the 1000 lines mm-1 grating and thick Lexan filter combination, and compared models with and without the spectral orders m = 6-20 included. Figure 3 shows the result of this comparison. Clearly, the excess seen at 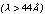 (E < 0.28 keV) is simply due to the higher orders of short-wavelength flux. No modifications to the efficiency model have to be made in order to obtain quantitative agreement with the measured fluxes.
(E < 0.28 keV) is simply due to the higher orders of short-wavelength flux. No modifications to the efficiency model have to be made in order to obtain quantitative agreement with the measured fluxes.
The new efficiencies are not likely to affect any of the analysis done on grating images other than those of Sco X-1. Probably only this source is bright enough to show dispersion into sixth and higher order above the background; but low-level 'excesses' at long wavelengths 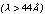 should be treated with caution in any case. Discrepancies may persist even with the new calibration, in view of the limitations of our model outlined in the previous section.
should be treated with caution in any case. Discrepancies may persist even with the new calibration, in view of the limitations of our model outlined in the previous section.
The only other datasets that are affected by the new grating efficiencies are the data taken with the 1000 lines mm-1 grating on AM Her. In the 80-100 Å wavelength range, gold has a local minimum in the absorption coefficient, and the bars of the 1000 lines mm-1 grating become partially transparent again, giving rise to a resonance-like feature in the efficiency curve. The exact shape and location of this feature is strongly dependent on the grating parameters. With the grating model developed above, we can now self-consistently calculate the efficiency curve in this wavelength band as well. None of the other strong soft X-ray sources observed with EXOSAT (the hot white dwarfs) were observed with the 1000 lines mm-1 grating.
Figure 3 1000 lines mm-1 TGS spectrum, thick Lexan filter, obtained in a 1 hr exposure on 1983/220; zero order and background subtracted (crosses). The solid histogram is a thermal bremsstrahlung model, at kT = 13.5 keV, column density of neutral absorbing material NH = 1.6 x 1021 cm-2 with the first 5 diffraction orders only included in the model (upper panel), and with 20 diffraction orders included (lower panel).
5 Future Work
In principle, the same treatment should be applied to the 500 lines mm-1 grating, and we plan to at least extend the efficiencies for this grating using a model based on the current best estimate for the parameters of the grating.
A version of the code that produces a grating spectrometer matrix for XSPEC, for an arbitrary number of spectral orders and each filter, will be implemented at the HEASARC in the near future.
A paper describing the grating efficiency recalibration in more detail is in preparation (Wolkovitch, Paerels, and Kahn 1992).
References
Brinkman, A.C., Dijkstra, J.H., Geerlings, W.F.P.A.L., van Rooijen, F.A., Timmerman, C., and de Korte, P.A.J., 1980, Appl. Opt., 19, 1601.
de Korte, P.A.J., Bleeker, J.A.M., den Boggende, A.J.F., Branduardi-Raymont, G., Brinkman, A.C., Culhane, J.L., Gronenschild, E.H.B.M., Mason, I., and McKechnie, S.P., 1981, Space Sci. Rev., 30, 495.
Henke, B.L., Lee, P., Tanaka, T.J., Shimabukuro, R.L., and Fujikawa, B.K., 1981, in: D.T. Attwood and B.L. Henke (Eds.), 'Low Energy X-ray Diagnostics', AIP Conference Proceedings No. 75 (AIP, New York).
Paerels, F.B.S., Brinkman, A.C., den Boggende, A.J.F., de Korte, P.A.J., and Dijkstra, J., 1990, Astron. Astrophys. Suppl., 85, 1021.
Wolkovitch, D.N., Paerels, F.B., and Kahn, S.M., 1992, Appl. Optics, in preparation.
 Proceed to the next article
Proceed to the next article  Return to the previous article
Return to the previous article

 Select another article
Select another article