NOTICE:This Legacy journal article was published in Volume 4, February 1994, and has not been updated since publication. Please use the search facility above to find regularly-updated information about this topic elsewhere on the HEASARC site. |
ROSAT PSPC
Off-Axis Point Spread Function
MPE/OGIP Calibration Memo CAL/ROS/93-015 Version: 1993 Sept 18
Summary
This article details the extension of the description of the point spread function of the ROSAT PSPC to include off-axis effects. We present the off-axis psf algorithm and compare the model to in-flight data We discuss the limitations of this parameterization with respect to data analysis.
1 The Data and Model
As detailed in CAL/ROS/92-001 (Hasinger et al. 1992, hereafter H92), the point spread function (psf) of the ROSAT X-ray mirror assembly (XMA) + PSPC is a convolution of 5 components:
1. The XMA scattering profile
2. The off-axis blur of the XMA
3. The intrinsic spatial resolution of the PSPC
4. Focus and detector penetration effects
5. A widening of the PSPC resolution due to the existence of 'Ghost images' (for PHA channels
< 20 only)
There is also some residual ellipsoidal blur due to residual attitude motion, but for the PSPC, this component is usually negligible compared to the other effects (see H92 for more details). The XMA scattering profile, the intrinsic spatial resolution of the PSPC, and focus and detector penetration effects have already been described in H92 and Hasinger et al. 1993. The psf was parameterized for on-axis observations from PANTER ground calibration measurements. In H92 it was shown that the derived analytical functions satisfactorily described 5 moderate signal-to-noise datasets in all but the softest band where 'Ghost Imaging' was already known to be a problem. Here we extend the treatment to include a parameterization of the change in shape of the psf with off-axis angle.
Examination of a bright point source observed off-axis reveals an asymmetry in the distribution of source counts that becomes easily noticeable once the source is observed outside of the central ring of the PSPC (i.e. > 20 arcmin off-axis). The asymmetry is produced because for off-axis irradiation half of the mirror sees a different grazing angle to the other. The two relatively sharp outer boundaries of the blur area, which have different radii of curvature, are produced by the front and rear aperture planes of the mirrors, respectively. The hole in the psf is due to the central hole in the mirror aperture (the mirror consists of three shells) defocused at large angles as the detector is flat but the focal plane is curved. The radial struts also interfere with the photon distribution as they shadow part of the detector. This combination produces the diffraction-like radial pattern seen on bright sources observed at large offset angles. Figure 1 shows the image of a source at an offset angle of 40 arcmin for a) inflight data and b) PANTER calibration data, where the center of the detector is towards the upper left hand side of the image in each case.
While early attempts to parameterize the change in shape of the psf concentrated on the ground calibration data taken at the PANTER facility, a comparison of those data with in-flight data showed significant differences. These differences are due to the finite source distance in the PANTER facility, which results in a beam divergence of about 10 arcmin. The consequence of this is that the PANTFR data have the hole on the inner side of the peak of counts for off-axis sources, while the in-flight data show the opposite effect (compare figures 1a and 1b). In addition, the PANTER image shows greater interference between the psf and the PSPC wire grid (effects which are reduced by the wobble of in-flight observations). As a consequence of these differences, in-flight data collected from a variety of bright serendipitous sources detected in pointed observations were finally used to parameterize the off-axis dependence of the psf, while the components which are independent of off-axis angle were carried over from the higher-quality on-axis data.
The off-axis blur of the telescope, although highly structured and asymmetric, has been modeled by a simple Gaussian for comparison to a azimuthally integrated profile. This Gaussian term for the off-axis blur is added in quadrature to the Gaussian term describing the intrinsic PSPC resolution. Since the model approximates the behavior of the detector by the addition of Gaussian, exponential and Lorentzian terms, instead of a mathematically correct convolution of terms, then we have to adjust the contribution of the other terms relative to the on-axis case, to allow for the off-axis behavior of the Gaussian term. The new term for the exponential fraction describes the relative diminishing of this term with increasing offset angle, due to the increase of the Gaussian term.
2 The Off-Axis Parameterization
Throughout,
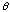 is the off-axis angle (in arcmin) from the center of the PSPC field of view,
is the off-axis angle (in arcmin) from the center of the PSPC field of view,
r is the radius (in arcmin) from the PSF centroid,
PSF(E,r,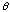 ) is the psf (in normalized cts arcmin2),
) is the psf (in normalized cts arcmin2),
and E is the photon energy (in keV).
2.1 The mirror scattering term
The analytical form derived for the fraction of photons within this component as a function of energy is given by:
Fscatt = 0.075 E+1.43 (1)
The increase in Fscatt with E is slower than the E2 powerlaw expected due to the detailed structure (micro-roughness) of the mirror surface.
As in the on-axis case, this steepens to a powerlaw at large r, i.e.
PSFscatt(E,r) = ![A_scatt (E) / [1 + (2r/r_scatt(E))^2]](pspc2-3.gif) for
for 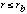 = PSF(E,rb) (r/rb)-
= PSF(E,rb) (r/rb)- for
for 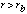 (2)
(2)
where
rb(E) = 861.9/60 E-1 arcmin (3)
and
 = 2.119 + 0.212E (4)
= 2.119 + 0.212E (4)
The width of the Lorentzian, rscatt, as a function of energy was found to be:
rscatt(E) = 79.9/60 E-1 arcmin (5)
The normalization of the Lorentzian, Ascatt, is given by
Ascatt = Fscatt(E) /  normalized cts arcmin-2 (6)
normalized cts arcmin-2 (6)
where
=
(rscatt/2)2 [ln (1 + (2/rscatt)2 rb2) + 2 rb2 ((rscatt/2)2 + rb2)-1
] (7)
is the renormalization factor such that [1]
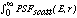 2
2 r dr = Fscatt(E) (8)
r dr = Fscatt(E) (8)
2.2 The exponential focus and penetration depth term
The analytical form derived for the fraction of photons within this component as a function of energy is given by whichever is the smaller of the following two terms:
Fexp(E, ) = 10-1.635+0.639E+0.052E2e-0.5(
) = 10-1.635+0.639E+0.052E2e-0.5( /12)2 (9)
/12)2 (9)
OR
Fexp(E, ) = 1.0 - Fscatt (10)
) = 1.0 - Fscatt (10)
Equation 10 is necessary to avoid the "exponential artifact" of H92 which made the psf parameterization invalid above 2 keV.
The combined contribution of focusing and the finite penetration of photons into the counter on the psf can still be modeled as an exponential function where r is the radial distance from the centroid position of the radial profile, in arcmin.
PSFexp(E,r) = Aexp(E) exp[-r/ (E)] normalized cts arcmin-2 (11)
(E)] normalized cts arcmin-2 (11)
The e-folding angle,  , was found to be the same as for the on-axis case
, was found to be the same as for the on-axis case
 (E) = 1/60 (50.61E-1.472+6.80E+5.62)1/2 arcmin (12)
(E) = 1/60 (50.61E-1.472+6.80E+5.62)1/2 arcmin (12)
The normalization, Aexp(E), is given by
Aexp(E) = Fexp(E)/(2 (
( (E))2) normalized cts arcmin2 (13)
(E))2) normalized cts arcmin2 (13)
and as for the other components has been normalized such that the integral of PSFexp(E,r) 2  r dr over the range
r dr over the range 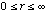 equals Fexp(E).
equals Fexp(E).
2.3 The Gaussian intrinsic resolution and mirror blur term
All photons not in the other 2 components are assumed to be in this component. Thus the fraction of photons within this component as a function of energy is given by:
Fint = 1 - Fscatt - Fexp (14)
Note that this becomes zero above 2 keV from equation 10.
PSFint(E,r) = Aint(E) exp(-1/2 (r/r (E))2) normalized cts arcmin-2 (15)
(E))2) normalized cts arcmin-2 (15)
The derived analytical form for the width of the detector Gaussian, G (E,
(E, ), as a function of energy is given by:
), as a function of energy is given by:
r (E) = 1/60 (108.7E-0.888 + 1.121E+6)1/2 arcmin (16)
(E) = 1/60 (108.7E-0.888 + 1.121E+6)1/2 arcmin (16)
The analytical form for the Gaussian mirror blur is
m (
( ) = 1/60 (0.219
) = 1/60 (0.219 2.848)1/2 arcmin (17)
2.848)1/2 arcmin (17)
These two Gaussian widths are combined as follows:
G (E,
(E, ) = r
) = r 2 + m
2 + m 2)1/2 (18)
2)1/2 (18)
The normalization, Aint(E), is given by
Aint(E) = Fint(E)/2 (G
(G (E))2) normalized cts arcmin-2 (19)
(E))2) normalized cts arcmin-2 (19)
where the denominator is the renormalization factor such that the integral of PSFint(E,r)2 r dr over the range
r dr over the range  equals Fint(E).
equals Fint(E).
Figure 2 compares the mirror Gaussian width m with the detector Gaussian width r
with the detector Gaussian width r versus angle
versus angle  . Figure 3 shows the total Gaussian width G
. Figure 3 shows the total Gaussian width G , versus angle. From these figures we see that above ~ 14 arcminutes, the mirror Gaussian term becomes dominant over the detector Gaussian term. Figure 4 shows the change of shape of the components of the psf with increasing off-axis angle, for 5 illustrative energies.
, versus angle. From these figures we see that above ~ 14 arcminutes, the mirror Gaussian term becomes dominant over the detector Gaussian term. Figure 4 shows the change of shape of the components of the psf with increasing off-axis angle, for 5 illustrative energies.
2.4 Test Results
The data shown here are a representative subset of the data used for testing the off-axis psf algorithm. Radial profiles were extracted centered on the source. When comparing the model and data at large angles (i.e. in the outer region of the PSPC) it was crucial to define the center of weight of the counts (which lies between the peak and hole) such that we could produce a radial average of these features in each bin. We used the IRAF imcntr routine (proto.imcntr). Given the approximate coordinates of the center of an object, imcntr will compute a more accurate center using the algorithms described in the Kitt Peak publication "Stellar Magnitudes from Digital Images" under the Mountain Photometry Code section. Briefly, this algorithm computes the sum of all the rows and the sum of all the columns in the extraction box. Because the centers are computed independently for x and y, the result may be considered inferior to a true two-dimensional centering algorithm, but in practice the results appear to be very usable.
The lowest 11 PI channels were rejected altogether to exclude problems due to the variable lower limit discriminator for valid events due to the variable instrument gain which is folded into these data. As described in H92, we do not expect an acceptable fit to be obtained in the B band, due to the "ghost imaging" effect. Additional sources falling within the specified annuli were masked out of the analysis. No background subtraction was carried out. Background rates were measured from the events file and were later added to the predicted profile template for each band. As in H92, a spectrum was also extracted for each source and the predicted model could then be appropriately weighted with source spectrum, for the energy band selected in each case. In addition, the model was weighted with the amount of time the source spent at each position on the detector, as the detector was wobbled across the sky during the observations.
3 Results
These predicted psf templates are overlaid on some sample datasets in Figure 5. We stress that the normalization of the model psf in each case was also calculated using the equations presented here, thus NO FITTING was performed. The normalization of the predicted psf was calculated such that the integral under the predicted template is equal to the integral under the observed psf.
It can be seen that even at this high signal-to-noise ratio, the psf model provides an acceptable parameterization of the source profile for all but the B-band (as expected). This model can be used to search for extended emission (the limits of accuracy are evident by comparison with the plots in Figure 5) and to determine the extraction cell required for spectral and timing analysis.
Conclusions
An acceptable model for the off-axis dependence of the ROSAT PSPC psf has been produced which can be used to estimate the correct extraction radii required for data analysis of off-axis sources. In addition, this can be used to determine whether off-axis sources are significantly extended. The plots provided illustrate the limits of the accuracy of this parameterization (particularly important for determination of significant extent) and PIs are invited to contact the GOF team if they wish to discuss any aspects of this parameterization. The comparison between model and data is most difficult for sources observed in the outer region of the PSPC detector, where radial profiles must be carefully centered to obtain meaningful results.
The contact person at GSFC is Jane Turner (turner@lheavx.gsfc.nasa.gov or LHEAVX::TURNER).
Acknowledgments
We thank Dave Davis for his help in the original extraction of some of the off-axis data.
References
Hasinger, G., Turner, T.J., George, I.M. & Boese, G., 1992. Legacy, 2, 77 (CAL/ROS/92-001).
Hasinger, G., Turner, T.J., George, I.M. & Boese, G., 1993. Legacy, 3, 46 (CAL/ROS/92-001a).
Figures 1a-b
a) The in-flight psf for a point source located 40' off-axis. The center of the detector is towards the upper left of the figure.
b) The PANTER psf for a point source located 40' off-axis. The center of the detector is towards the upper left of the figure.
Figure 2 The widths of the mirror (m[[sigma]]) and detector (r[[sigma]]) components to the Gaussian term. This illustrates how the mirror effect begins to dominate outside of ~ 14 arcminutes. The lines of constant detector component represent (from top to bottom) 0.28, 0.50, 2.0 and 1.0 keV. (The detector Gaussian has a minimum between 1 and 2 keV, as detailed in Hasinger et al. 1992, thus the inversion.)
Figure 3 The width of the mirror + detector Gaussian term versus off-axis angle. The lines represent (from top to bottom) 0.28, 0.50, 2.0 and 1.0 keV. (The detector Gaussian has a minimum between 1 and 2 keV, as detailed in Hasinger et al. 1992, thus the inversion.)
Figures 4a-e
a) The components of the PSPC psf versus off-axis angle at 0.188 keV.
b) The components of the PSPC psf versus off-axis angle at 0.284 keV.
c) The components of the PSPC psf versus off-axis angle at 0.5 keV.
d) The components of the PSPC psf versus off-axis angle at 1.0 keV.
e) The components of the PSPC psf versus off-axis angle at 1.7 keV.
 Proceed to the next article
Proceed to the next article  Return to the previous article
Return to the previous article

 Select another article
Select another article